Uniform Manifold Approximation and Projection

Uniform Manifold Approximation and Projection(UMAP), much like t-SNE, has the goal of modeling the distances between points in high-dimensional space in a lower-dimensional space, while preserving local structure. However, UMAP is generally faster and scales better to large datasets compared to t-SNE, while also preserving more of the global structure of the data. It does this by attemping to build a graph model instead of a gaussian like SNE.

Unlike both Principle Component Analysis and T-distributed stochastic neighbor embedding, UMAP has an exceptional ability to preserve the structure of the data in a way where you can understand the higher dimensional shape. A great example is mapping a 3d point cloud of a familiar object (like a mammoth) to $R^{2}$ :

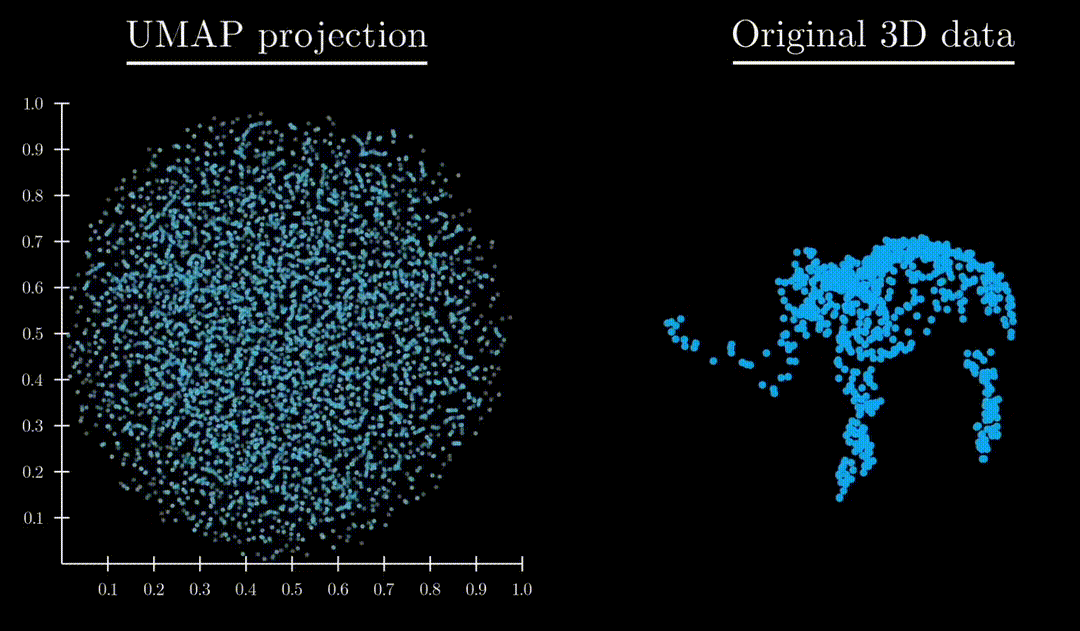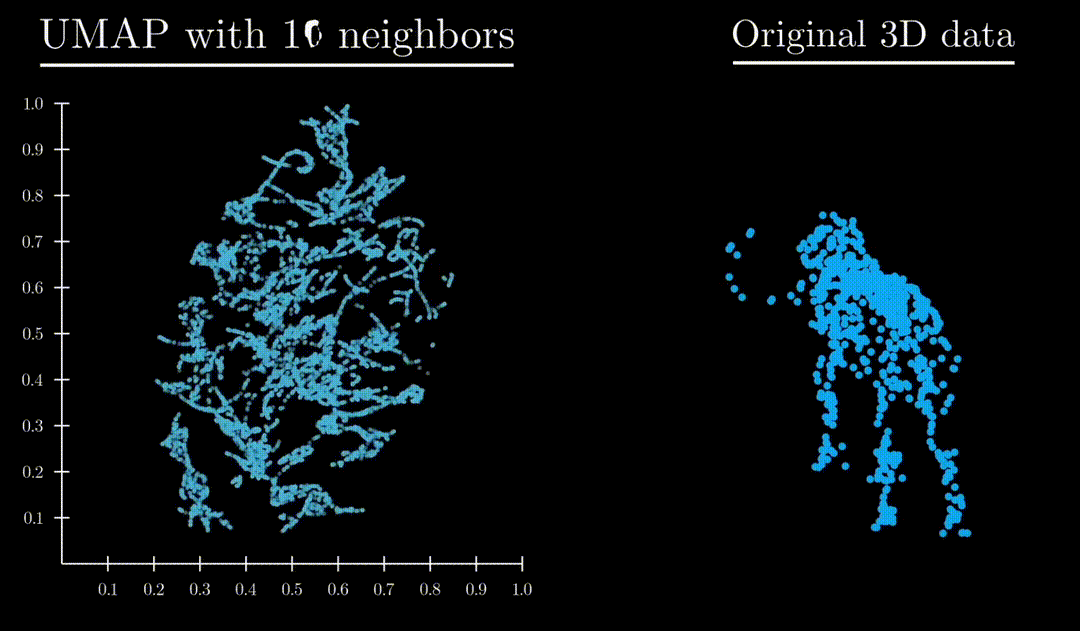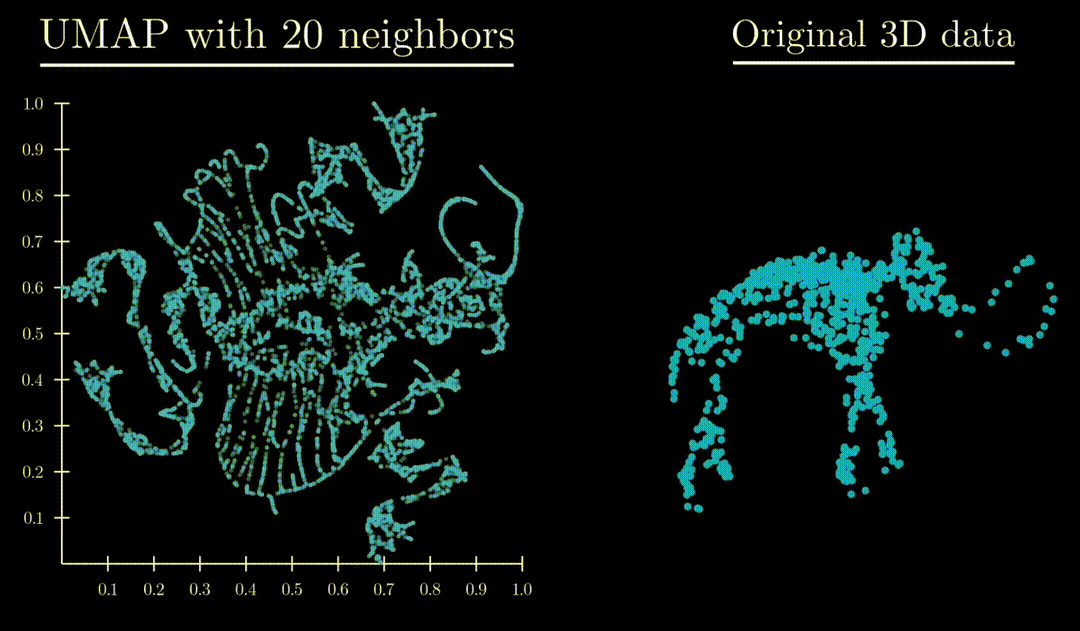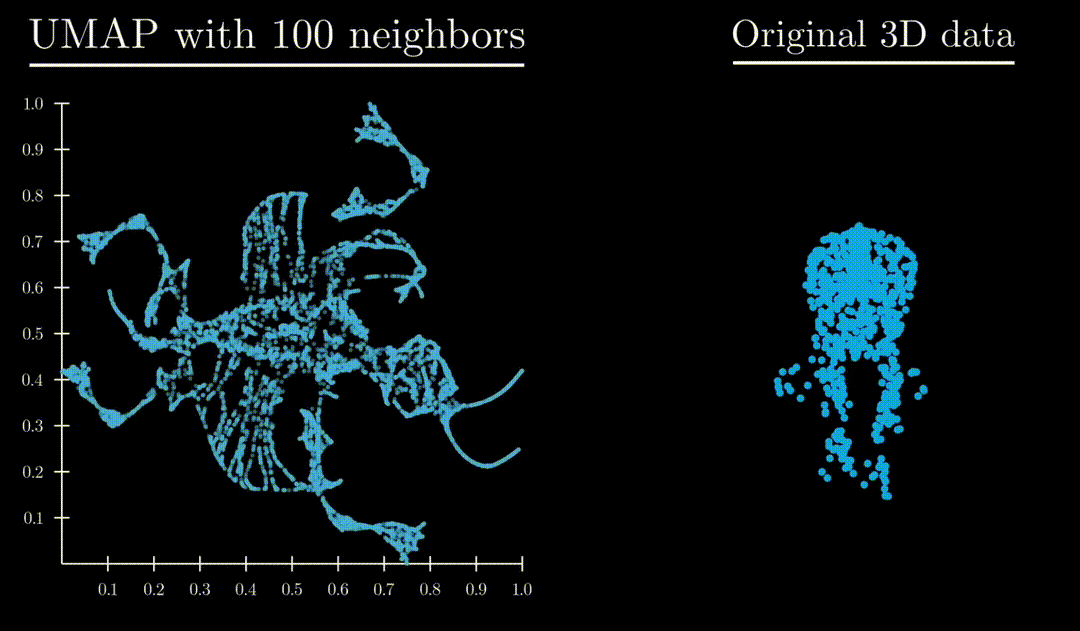
Formulation

UMAP is grounded in Riemannian geometry and algebraic topology, specifically the theory of fuzzy simplicial sets. While the full mathematical framework is complex, the algorithmic implementation can be understood in terms of graph construction and optimization.

Graph Construction

UMAP first constructs a weighted k-nearest neighbor graph in the high-dimensional space. For each point $x_{i}$ , we find its $k$ nearest neighbors and compute edge weights using an exponential kernel with adaptive bandwidth:

w (x_{i}, x_{j}) = exp (- \frac{max ( 0 , d ( x _{i} , x _{j} ) - ρ _{i} )}{σ _{i}})

where:

$d (x_{i}, x_{j})$ is the distance between points
$ρ_{i}$ is the distance to the nearest neighbor of $x_{i}$ (ensures local connectivity)
$σ_{i}$ is a normalization factor chosen so that $\sum_{j} w (x_{i}, x_{j}) = lo g_{2} (k)$

The weights are then symmetrized using a fuzzy set union:

w_{ij} = w (x_{i}, x_{j}) + w (x_{j}, x_{i}) - w (x_{i}, x_{j}) \cdot w (x_{j}, x_{i})

Low-Dim Representation

In the low-dimensional space, UMAP uses a probability distribution based on the distance between embedded points $y_{i}$ and $y_{j}$ :

q_{ij} = (1 + a \cdot ∣∣ y_{i} - y_{j} ∣ ∣^{2 b})^{- 1}

where $a$ and $b$ are hyperparameters controlling the shape of the embedding (typically $a \approx 1.93$ and $b \approx 0.79$ for 2D embeddings). These are determined by the min_dist parameter, which controls how tightly points can be packed together.

Optimization Objective

UMAP minimizes the Cross Entropy between the high and low-dimensional representations:

C = i, j \sum w_{ij} lo g (\frac{w _{ij}}{q _{ij}}) + (1 - w_{ij}) lo g (\frac{1 - w _{ij}}{1 - q _{ij}})

This is optimized using stochastic gradient descent with negative sampling for efficiency. The gradient with respect to the low-dimensional coordinates is:

\frac{\partial C}{\partial y _{i}} = j \in N (i) \sum \frac{- 2 ab ∣∣ y _{i} - y _{j} ∣ ∣ ^{2 b - 2}}{1 + a ∣∣ y _{i} - y _{j} ∣ ∣ ^{2 b}} (y_{i} - y_{j}) w_{ij} - j \in / N (i) \sum \frac{2 b}{( 0.001 + ∣∣ y _{i} - y _{j} ∣ ∣ ^{2} ) ( 1 + a ∣∣ y _{i} - y _{j} ∣ ∣ ^{2 b} )} (y_{i} - y_{j}) (1 - w_{ij})

where $N (i)$ denotes the neighbors of $i$ .

Main Hyperparameters

$n_{n e i g hb ors}$ : Controls locality/size of neighborhood clusters. Small values focus on local substructure, high values mean more global structure captured.

$min - d i s t$ : minimum value between points in low dim space.

Use when

You want to get a sense of global/local structure like t-SNE, without the huge performance cost. However, it is still vulnerable to hyperparameter sensitivity, where outputs may differ greatly through tiny changes to inputs.

Some Use Cases in Computational Neuroscience

UMAP has become increasingly popular in neuroscience for:

Neural population analysis: Visualizing high-dimensional neural state spaces
Single-cell RNA-seq: Clustering and trajectory inference in genomic data
Spike train embeddings: Revealing structure in population firing patterns
Behavioral manifolds: Mapping high-dimensional behavioral recordings to interpretable spaces

Graph View