Self Attention

Assuming that we are working with a Large Language Model, and as such we have already associated an Embedding Vector to each Token based on its learned value and its position, the next logical step would be to allow these new vectors to “soak up” more knowledge about the words around them.

$$Token[\text{"Tower"}]\to \left[\begin{array}{c}\stackrel{\text{position}}{\overbrace{0}}\\ 62.8\\ 8.2\\ -100.1\\ ⋮\\ 19.7\end{array}\right]$$

¹

This is necessary as right now, these vectors only contain a 1-to-1 correspondence for the word they represent, with no regard for the context of the sentence, which can vastly change the meaning:

this case is a ${\mathbb{R}}^2$ mapping of the vector space, in practice this is extremely high dimensional embedding

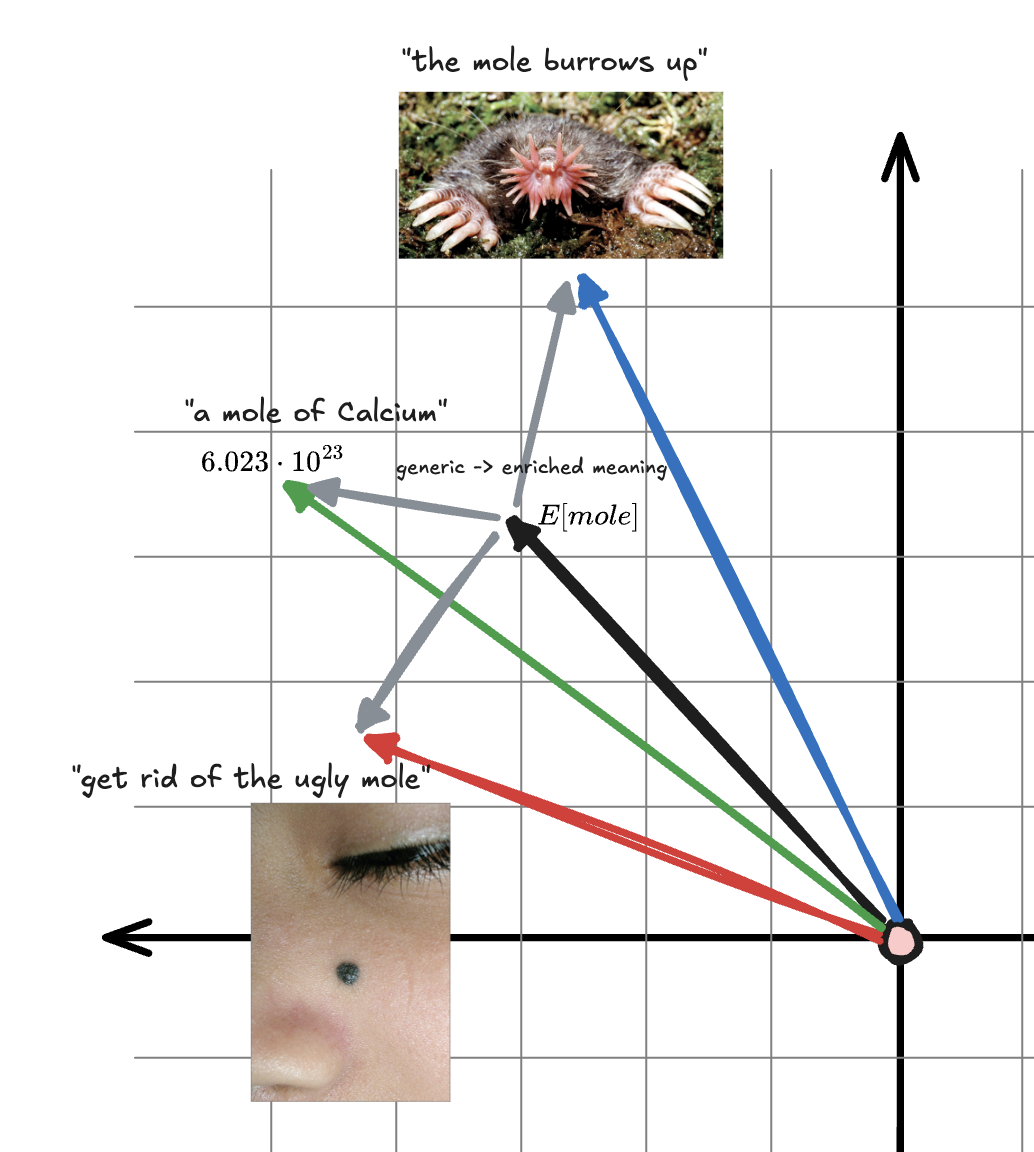
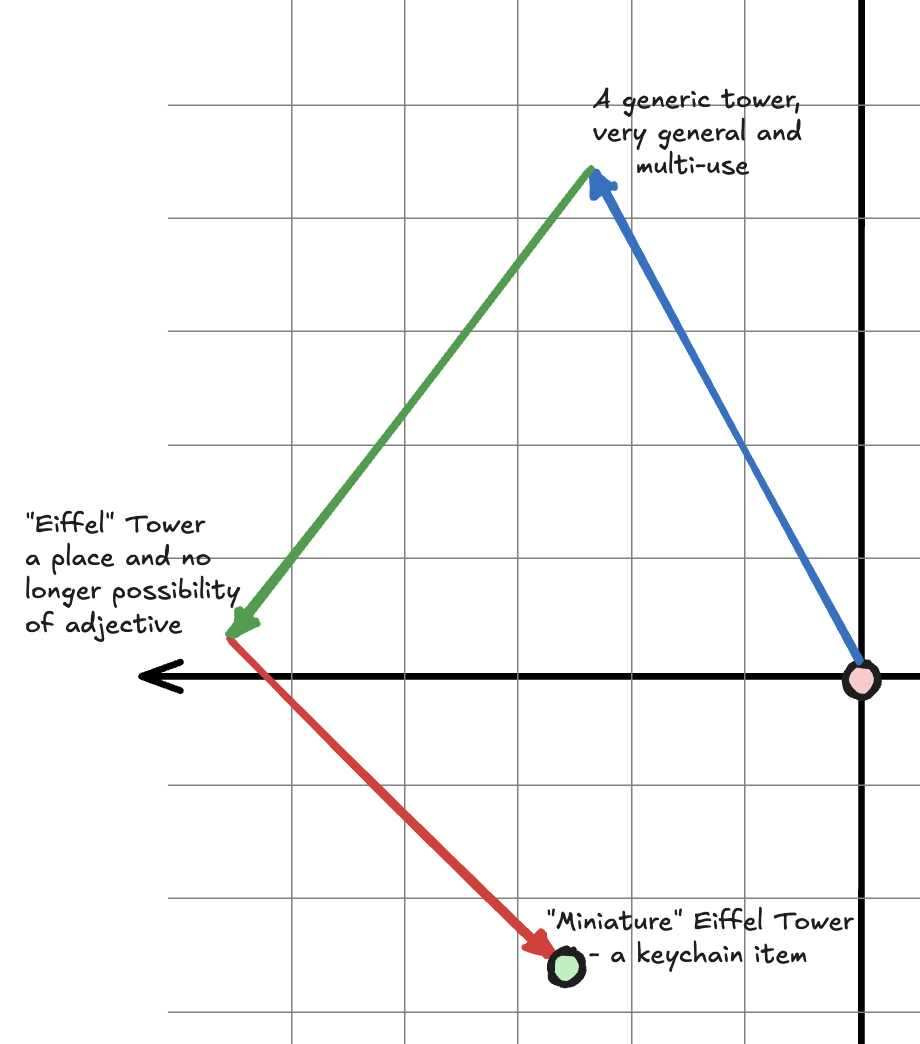
One might imagine that as the process of attention takes place, some “path” is taken into an incrementally more specific and rich context in this high dimensional space.

---

Key-Query-Value Matrices

Given some sentence we are looking embed the meaning of:

$$\begin{array}{cccccccccc}The& quick& brown& fox& jumps& over& the& lazy& dog& \\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \\ \left[\begin{array}{c}0.2\\ 57.6\\ ⋮\\ -87.2\end{array}\right]& \left[\begin{array}{c}7.2\\ 51.6\\ ⋮\\ 28.1\end{array}\right]& \left[\begin{array}{c}0.3\\ 9.6\\ ⋮\\ 19.1\end{array}\right]& \left[\begin{array}{c}0.7\\ 2.6\\ ⋮\\ 73.2\end{array}\right]& \left[\begin{array}{c}8.2\\ -57.6\\ ⋮\\ -10.2\end{array}\right]& \left[\begin{array}{c}1.2\\ 7.6\\ ⋮\\ 87.9\end{array}\right]& \left[\begin{array}{c}-0.2\\ 50.6\\ ⋮\\ 17.2\end{array}\right]& \left[\begin{array}{c}-0.2\\ 51.6\\ ⋮\\ 17.2\end{array}\right]& \left[\begin{array}{c}0.2\\ 17.6\\ ⋮\\ -17.2\end{array}\right]& \end{array}$$

How can we allow each to “influence” meaning of each other, in a way where we end up with a vector embedding representing the whole sentence?

Initial intuition might lead you to try adding all the vectors together to form a “path” of a sentence, and while this is in the right direction of our end goal, this has no regard for relative importance of the words in the sentence.

For example, the second “the” has no real affect on the meaning of the brown fox. Simply adding the vectors together would not capture these complicated semantic dynamics.

Another approach could be using a Parse Tree to structurally represent the sentence by labeling of subjects vs predicates, etc. While this has been a technique in papers investigating Diffusion as a Language Modeling technique,² Transformers make use of something new altogether.

To start, we introduce something called the Query Matrix. This can be thought of as every token asking every other token “hey, how much do you relate to me?“. Each token in our vocabulary will have its own own learned matrix parameters, in the case of GPT3 this was a 128 dimensional vector.

To get this query vector, the embedding of the token is multiplied by a learned matrix $W_Q$, which then yields the query vector for that token, ${\vec{Q}}_i$:

$$\underset{\text{learned matrix}}{\underbrace{W_Q}}\times \underset{\text{token embedding}}{\underbrace{{\vec{E}}_i}}=\underset{\text{Resultant Query Matrix}}{\underbrace{{\vec{Q}}_i}}$$

Think of this much smaller dimensional vector as encoding a notion of “looking for important words”, for which ones that matter to that word will match nicely with.

How this comparison is executed is with another $128$ dimensional matrix, the Key Matrix. This is computed in much the same way, taking another learned matrix $W_K$ that is again multiplied with the token embedding to achieve another lowed dimension vector. Think of this as the “answer” to the question that is the query.

$$W_K\times {\vec{E}}_i={\vec{K}}_i$$

The next step is quite trivial, we compute how well a key matches with a value by performing a cosine similarity test, or in simpler terms, just taking the dot product of the two.

	The	quick	brown	fox	jumps	over	the	lazy	dog
The	${\vec{Q}}_1\cdot {\vec{K}}_1$	${\vec{Q}}_1\cdot {\vec{K}}_2$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	${\vec{Q}}_1\cdot {\vec{K}}_n$
quick	${\vec{Q}}_2\cdot {\vec{K}}_1$	${\vec{Q}}_2\cdot {\vec{K}}_2$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	${\vec{Q}}_2\cdot {\vec{K}}_n$
brown	$⋮$	$⋮$							$⋮$
fox	$⋮$	$⋮$							$⋮$
jumps	$⋮$	$⋮$							$⋮$
over	$⋮$	$⋮$							$⋮$
the	$⋮$	$⋮$							$⋮$
lazy	$⋮$	$⋮$							$⋮$
dog	${\vec{Q}}_n\cdot {\vec{K}}_1$	${\vec{Q}}_n\cdot {\vec{K}}_2$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	${\vec{Q}}_n\cdot {\vec{K}}_n$

Please Note

In this case, we are modeling for a single head attention mechanism. In practice, this is often scaled up to multi head attention to utilize parallelization as much as possible.

There is one more step in this process, and that is to take the Softmax of every column of the “table” we have created.

$$Softmax(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$

This means that every column will contain a series of values somewhere $0\le j\le 1$, where each column’s values will add up to $1$.

What we have essentially created here is a probability distribution for each words’ relative importance to every other word.

This is where the final step of the attention block comes in: the Value Matrix.

This is again computed in the same way as the query and key matrices, with its own learned matrix $W_V$:

$$W_V\times {\vec{E}}_i={\vec{V}}_i$$

The value matrix will be a lot bigger in shape than the previous two

$$\dots$$

As defined in the now famous paper Attention is All You Need,³ this whole process is represented as one “trivial” equation:

$$Attention(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

---

Extending to Multi-Headed Attention

$$todo\dots$$

Footnotes

1. In practical cases, position would be embedded in a much more abstract way than just having its index at the top. We will also be representing all tokens as full words for brevity ↩

2. Li, X. L., Thickstun, J., Gulrajani, I., Liang, P., & Hashimoto, T. B. (2022). Diffusion-LM Improves Controllable Text Generation (No. arXiv:2205.14217). arXiv. https://doi.org/10.48550/arXiv.2205.14217 ↩

3. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2023). Attention Is All You Need (No. arXiv:1706.03762). arXiv. https://doi.org/10.48550/arXiv.1706.03762 ↩