Turing Machines

Turing Machines are the next step in the evolution of automata. They are a theoretical model of computation that can simulate any algorithm.

---

Definitions

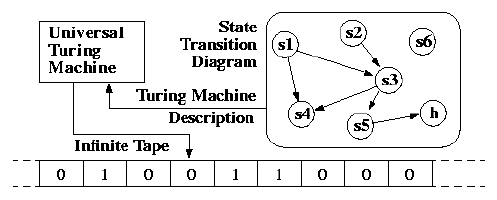
Before we get into the mathematical definition, let’s explore what a Turing Machine would look like in the physical world.

The simple idea of a turing machine is just a tape with a read/write head. The tape is infinite in both directions, and the read/write head can move left or right. The tape is divided into cells, each of which can hold a symbol from a finite set of symbols.

We can define a Turing Machine as a 7-tuple:

$$M=(Q,\Sigma ,\Gamma ,\delta ,q_0,q_{accept},q_{reject})$$

Where:

• Q is a finite set of states
• $\Sigma$ is a finite set of input symbols (input alphabet)
• $\Gamma$ is a finite set of tape symbols (tape alphabet)
• $\delta$ is the transition function
• $q_0$ is the initial state
• $q_{accept}$ is the accept state
• q_{reject} is the reject state

But we already know most of this from previous automata. The new part is the transition function, which is defined as:

$$\delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R\}$$

There are also multiple Turing Machine Variants, but that is for another time.

---

Transition Function in Depth

The transition function $\delta$ takes the current state and the symbol under the read/write head as input, and produces a new state, a symbol to write on the tape, and a direction to move the read/write head (left or right).

We can represent the transition function as a table:

$$\begin{array}{ccccc}\text{Current State}& \text{Read Symbol}& \text{New State}& \text{Write Symbol}& \text{Direction}\\ q_0& 0& q_1& 1& R\\ q_0& 1& q_2& 0& L\\ q_1& 0& q_0& 0& R\\ q_1& 1& q_1& 1& R\end{array}$$

This table tells us that if the machine is in state $q_0$ and reads a 0, it will transition to state $q_1$, write a 1 on the tape, and move the read/write head to the right.