Stable and Unstable Manifolds

Continuing from last lecture:

What about stability of period $k$ points in ${\mathbb{R}}^2$?

For $a=0.43,b=0.4$, there is a period-2 orbit given by:

$$\{(0.7,-0.1),(-0.1,0.7)\}$$

To check stability, we could compute the Jacobian of ${\vec{f}}^2$ or multiply Jacobians of $f$ at both points:

$$\begin{array}{rl}\mathcal{D}{\vec{f}}^2(\vec{x})& =\mathcal{D}\vec{f}(\vec{f}(\vec{x}))\cdot \mathcal{D}{\vec{f}}^2(\vec{x})\\ \mathcal{D}{\vec{f}}^2((0.7,-0.1))& =\mathcal{D}\vec{f}((-0.1,0.7))\cdot \mathcal{D}\vec{f}((0.7,-0.1))\\ & =\underset{\text{eigenvalues }\approx 0.26\pm 0.3i}{\underbrace{\left[\begin{array}{cc}0.12& 0.08\\ -1.4& 0.4\end{array}\right]}}\end{array}$$

This implies that the period-2 orbit is a sink.

---

Stable and Unstable Manifolds

Lets consider the linear map $f(x,y)=(\frac{2x,y}{2})$:

$$orA=\left[\begin{array}{cc}2& 0\\ 0& \frac{1}{2}\end{array}\right]$$

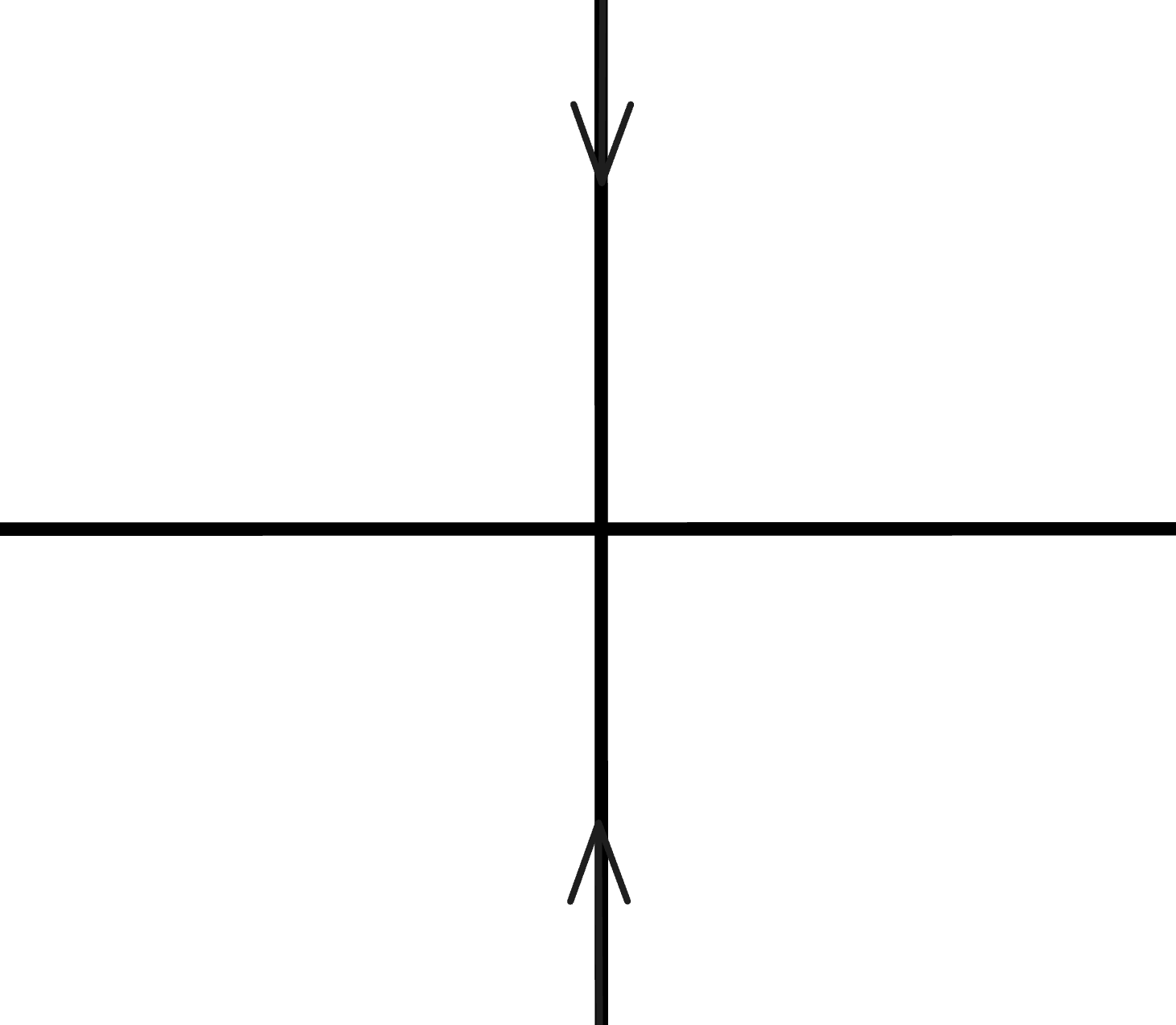
Points on the y-axis see origin as a sink. But we know it is a saddle. ${\lambda }_1=2,{\lambda }_2=\frac{1}{2},{\vec{v}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right],{\vec{v}}_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$

$"\\usepackage{tikz}\n\\usetikzlibrary{arrows.meta}\n\\begin{document}\n\\begin{tikzpicture}[scale=1.4, >=Stealth]\n \\draw[->, thin, gray] (-2.5,0) -- (2.5,0) node[right, black] {$x$};\n \\draw[->, thin, gray] (0,-2.5) -- (0,2.5) node[above, black] {$y$};\n\n$

source code

The y-axis is a Stable Manifold

The x-axis is a Unstable Manifold

We say a map $\vec{f}$ on ${\mathbb{R}}^m$ is one-to-one if:

$$\vec{f}({\vec{v}}_1)=\vec{f}({\vec{v}}_2)\Rightarrow {\vec{v}}_1={\vec{v}}_2$$

If a function is one-to-one, then its inverse map is also a function $f^{-1}$, e.g.:

$$f^{-1}(x,y)=(y,2x)$$

Let $\vec{f}$ be a smooth 1-1 map on ${\mathbb{R}}^2$ and let $\vec{p}$ be a Saddle fixed point (or periodic saddle point)…

Definition

The Stable Manifold of $\vec{p}$, call it $S(\vec{p})$, is the set of points $\vec{v}$ such that:

$$|{\vec{f}}^n(\vec{v})-{\vec{f}}^n(\vec{p})|\to 0asn\to \infty$$

The Unstable Manifold of $\vec{p}$, call it $U(\vec{p})$, is the set of points $\vec{v}$ such that

$$|{\vec{f}}^{-n}(\vec{v})-{\vec{f}}^{-n}(\vec{p})|\to 0asn\to \infty$$