Sinks, Sources, and Saddles

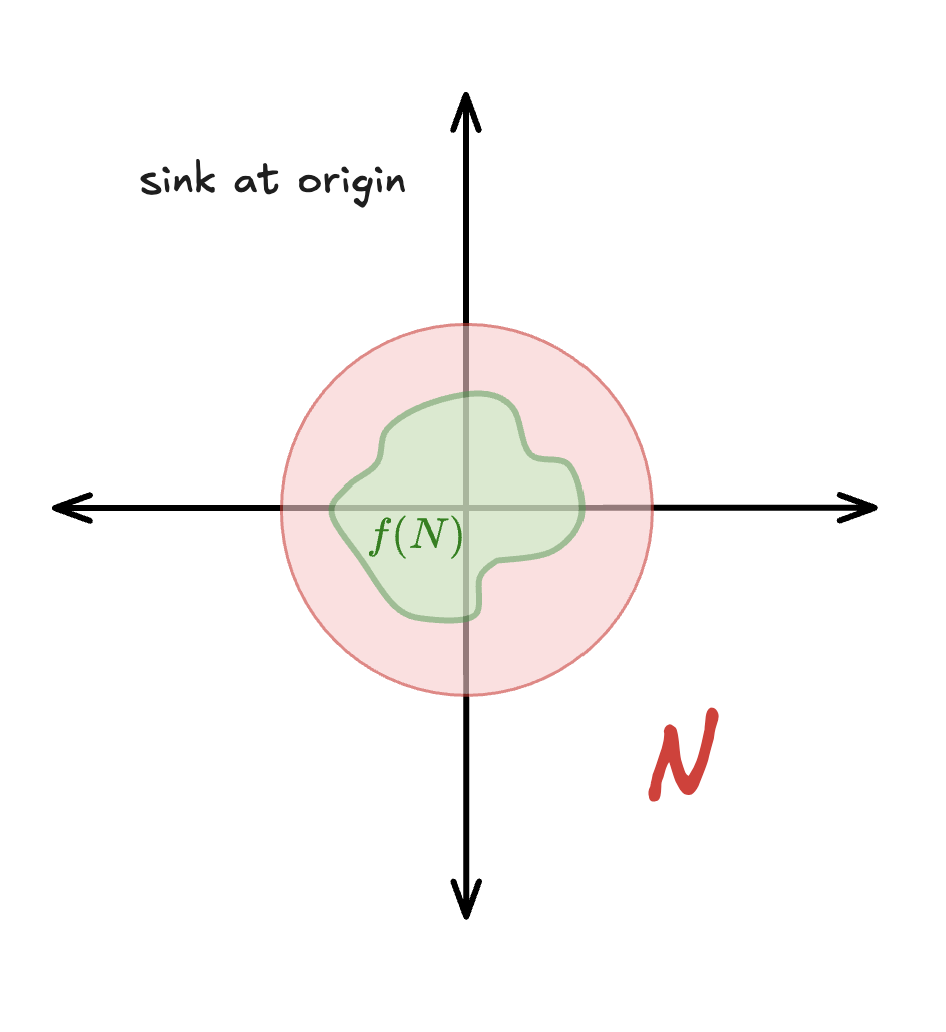
Sink at Origin (Stable Fixed Point)

A neighborhood N (red circle) centered at the origin contracts under the map f to a smaller region f(N) (green irregular shape) strictly contained within N.

At a sink, both eigenvalues of the Jacobian have absolute value less than 1. Under iteration of the Hénon Map $x_{n+1}=1-a{x}_n^2+y_n$, $y_{n+1}=b{x}_n$, trajectories starting in a neighborhood of the fixed point spiral inward. The contraction is visible as $f(N)\subset N$, indicating the basin of attraction. For the Hénon Map, this occurs when the parameters $(a,b)$ satisfy conditions where $|{\lambda }_1|,|{\lambda }_2|<1$.

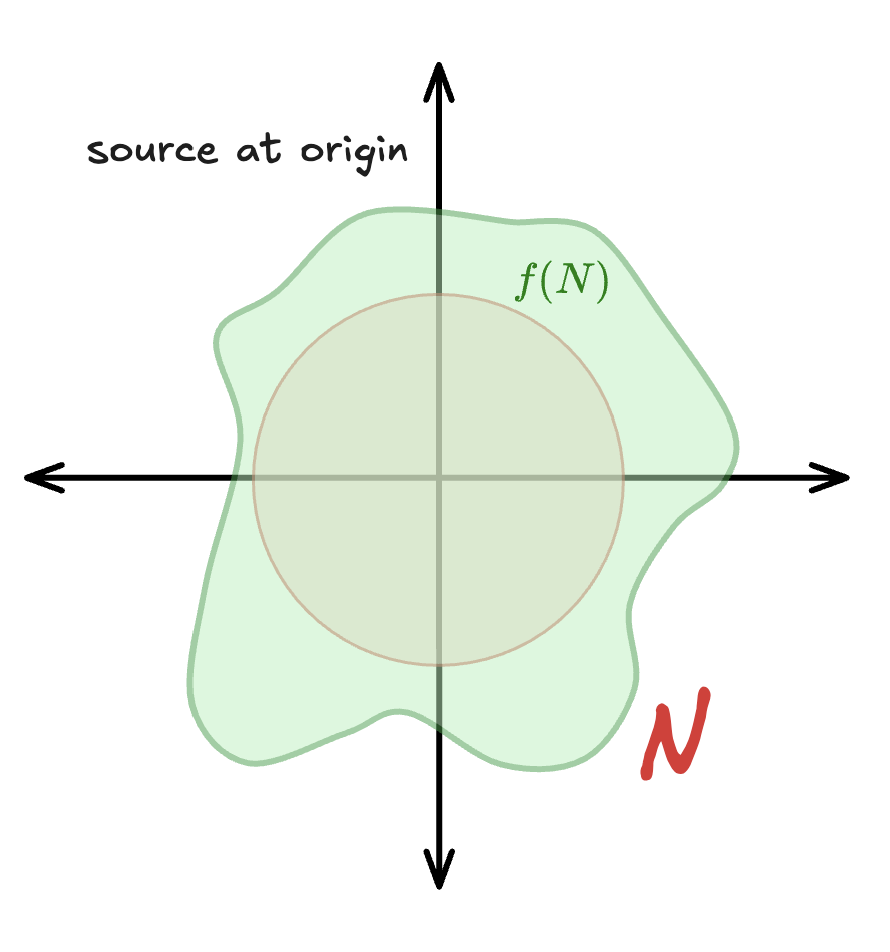
Source at Origin (Unstable Fixed Point - Repeller)

A neighborhood N (tan/beige inner circle) expands under the map to a larger region f(N) (green irregular shape) that extends beyond the original neighborhood.

At a source, both eigenvalues have absolute value greater than 1. Trajectories flow away from the fixed point in all directions. The expansion $f(N)\supset N$ shows that nearby points are pushed outward under iteration. In the Henon map, this behavior is time-reversed from a sink - if you ran the dynamics backward, a source would become a sink.

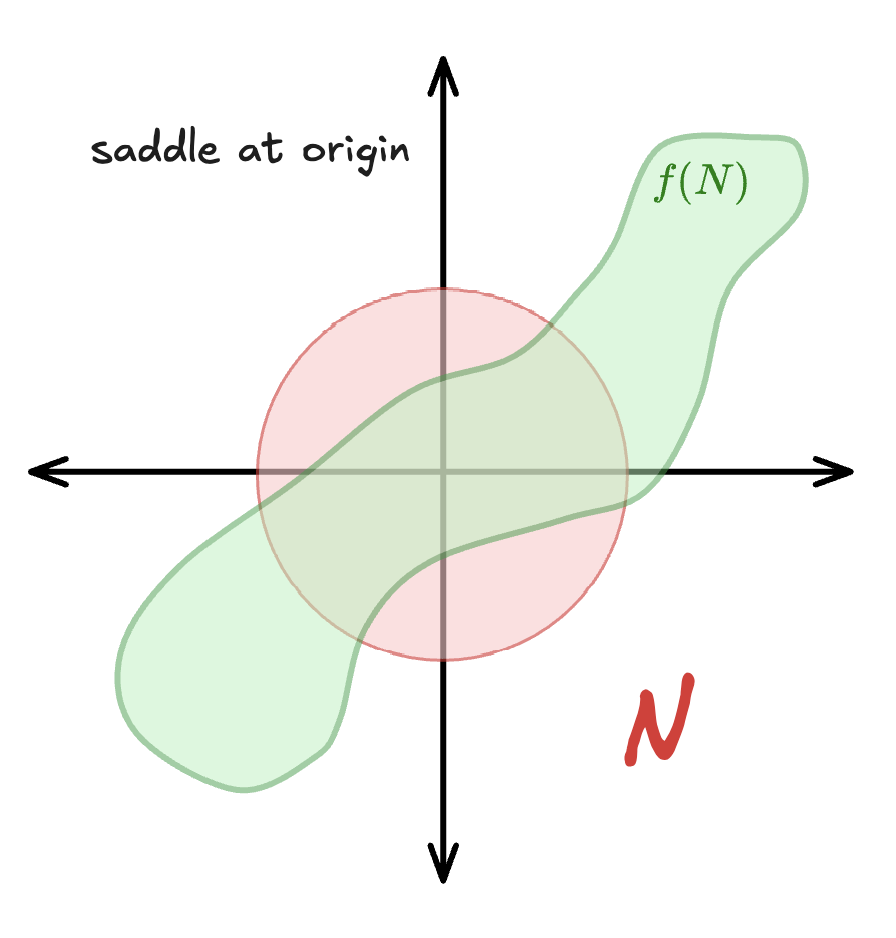
Saddle at Origin (Hyperbolic Fixed Point)

A neighborhood N experiences both contraction and expansion. The red region shows the stable manifold (attracting direction), while the green lobes of f(N) show the unstable manifold (repelling direction). The image stretches along one axis while contracting along another.

At a saddle point, one eigenvalue has $|{\lambda }_1|<1$ (stable direction) and the other has $|{\lambda }_2|>1$ (unstable direction). This is the most common and important case for the Henon map in its chaotic regime. The stable manifold (red) represents the set of points that approach the fixed point under forward iteration, while the unstable manifold (green lobes) represents points that approached the fixed point under backward iteration. The characteristic saddle topology - stretching in one direction, contracting in another - is fundamental to the horseshoe dynamics and chaotic behavior of the Henon map.

---

Linear Maps

A map $A(\vec{v})$ from ${\mathbb{R}}^n\to {\mathbb{R}}^m$ is linear if for each $a,b\in \mathbb{R}$ and $\vec{v},\vec{w}\in {\mathbb{R}}^m$:

$$A(a\vec{v}+b\vec{w})=aA(\vec{v})+bA(\vec{w})$$

Scaling and adding vectors before applying the map is the same as applying the map first and then scaling and adding the results.

The action of a linear map can be represented by multiplciation with an $m\times m$ matrix.

So… if ${\vec{v}}_0$ is an eigenvector of a matrix $A$ with an eigenvalue $\lambda$, then:

$${\vec{v}}_1=A{\vec{v}}_0=\lambda {\vec{v}}_0$$ $${\vec{V}}_2=A^2{\vec{v}}_0=A(\lambda {\vec{v}}_0)=\lambda A{\vec{v}}_0={\lambda }^2{\vec{v}}_0$$

Applying the linear map $A$ to an eigenvector ${\vec{v}}_0$ simply scales the vector by the eigenvalue $\lambda$. Repeated applications of $A$ scale the vector by successive powers of $\lambda$.

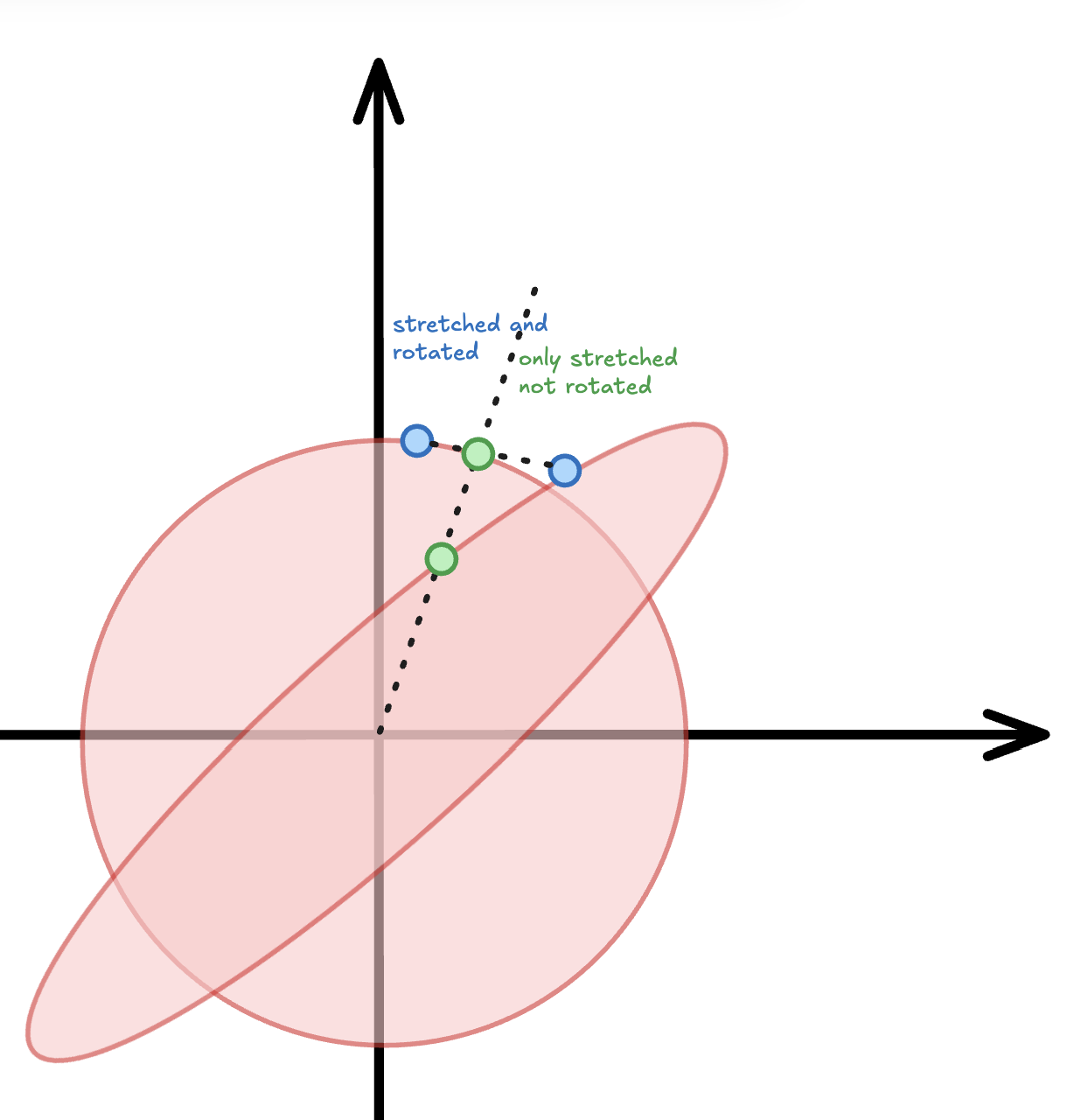
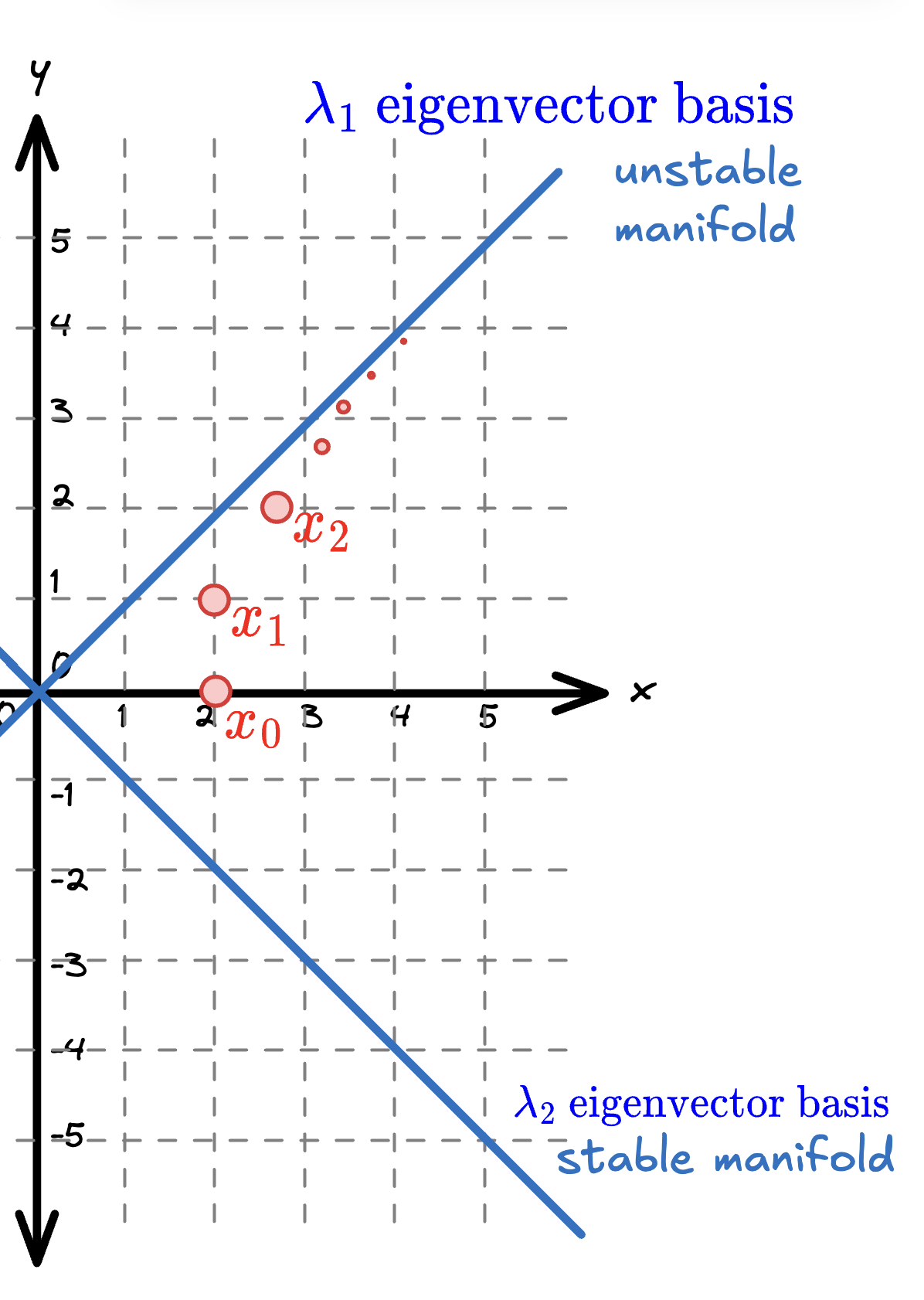
Say we have the matrix:

$$A=\left[\begin{array}{cc}1& \frac{1}{2}\\ \frac{1}{2}& 1\end{array}\right]{\vec{v}}_1=\left[\begin{array}{c}1\\ 1\end{array}\right]{\vec{v}}_2=\left[\begin{array}{c}1\\ -1\end{array}\right]{\lambda }_1=\frac{3}{2},{\lambda }_2=\frac{1}{2}$$

Iterating the map:

$${\vec{x}}_0=\left[\begin{array}{c}2\\ 0\end{array}\right]$$ $${\vec{x}}_1=A{\vec{x}}_0=\left[\begin{array}{cc}1& \frac{1}{2}\\ \frac{1}{2}& 1\end{array}\right]\left[\begin{array}{c}2\\ 0\end{array}\right]=\left[\begin{array}{c}2\\ 1\end{array}\right]$$ $${\vec{x}}_2=A{\vec{x}}_1=\left[\begin{array}{cc}1& \frac{1}{2}\\ \frac{1}{2}& 1\end{array}\right]\left[\begin{array}{c}2\\ 1\end{array}\right]=\left[\begin{array}{c}2.5\\ 2\end{array}\right]$$ $$\dots$$

Yields:

Starting from ${\vec{x}}_0=(2,0)$, successive iterations climb along the ${\lambda }_1$ eigenvector direction (unstable manifold). Since ${\lambda }_1=\frac{3}{2}>1$, points expand along this direction. The ${\lambda }_2$ eigenvector basis forms the stable manifold - points on this line contract toward the origin since ${\lambda }_2=\frac{1}{2}<1$.

The trajectory reveals the saddle structure: expansion along one eigendirection, contraction along the other. Notice how ${\vec{x}}_0$, ${\vec{x}}_1$, and ${\vec{x}}_2$ progressively move away from the origin along the diagonal (unstable manifold). Any initial condition not precisely on the stable manifold will eventually be repelled along the unstable direction - this is why saddles are sensitive to initial conditions

Same holds true for the Hénon Map saddle with their eigenvalue-manifold relationship. Points approach the fixed point along the stable manifold and are ejected along the unstable manifold. In chaotic systems like Henon, these manifolds fold and intersect in fractal patterns, creating the complex attractor structure.