Automatic Differentiation

Automatic differentiation (AD) is a computational technique used to evaluate the derivative of a function specified by a computer program. It is particularly useful in machine learning and optimization tasks, where gradients are needed for algorithms like gradient descent.

In Layman’s terms, automatic differentiation is like a smart calculator that can compute how much a function changes when you change its inputs, without needing to do the math by hand. It does this by breaking down the function into smaller parts and applying the chain rule of calculus automatically.

We will explore the above image in more detail in the next section.

---

Computing Derivatives Efficiently

In the context of machine learning algorithms like Gradient Descent, there exists a need for an efficient method for computing the derivatives of functions.

What one might think to do from high school calculus is to manually code out the derivative and call it a day.

$$f(x)=e^{2x}-x^3\to f^{\prime }(x)=2e^{2x}-3x^2$$

Becomes:

Python

import numpy as np def f(x): return np.exp(2*x) - x**3 def f_prime(x): return 2*np.exp(2*x)-3*x**2 print(f(10)) print(f_prime(10))

Output

However, this gets quite tedious for complicated functions. We need an automated approach.

Some Automated Approaches

There are several others ways for automating differentiation, Automatic Differentiation just happens to be one of these methods.

Numerical Differentiation

Numerical Differentiation uses finite differences to approximate the derivative. The simplest definition of this comes from the limit definition of the derivative.

$$f:{\mathbb{R}}^n\to \mathbb{R}$$

For a partial derivative, we set up something like the following:

$$\frac{\partial f}{\partial x_i}\approx \frac{f(x+h\stackrel{i_{th}\text{ unit vector}}{\overbrace{e_i}})-f(x)}{\underset{\text{step size}}{\underbrace{h}}}$$

Where $e_i$ is just the unit vector along the $i_{th}$ axis, and $h$ is the step size(usually a very small fraction).

While this method is a simple one, some issues arise with accuracy and numerical stability.

One of these possible issues involves truncation error; we are trying to approximate a limit as ${\lim }_{h\to 0}$, but we are using some nonzero $h$. The tangent line will approach a decreasing truncation error, but this eventually leads to a new issue of rounding error, involving floating point arithmetic.

When using this approach we will have to balance these two for the best minimum:

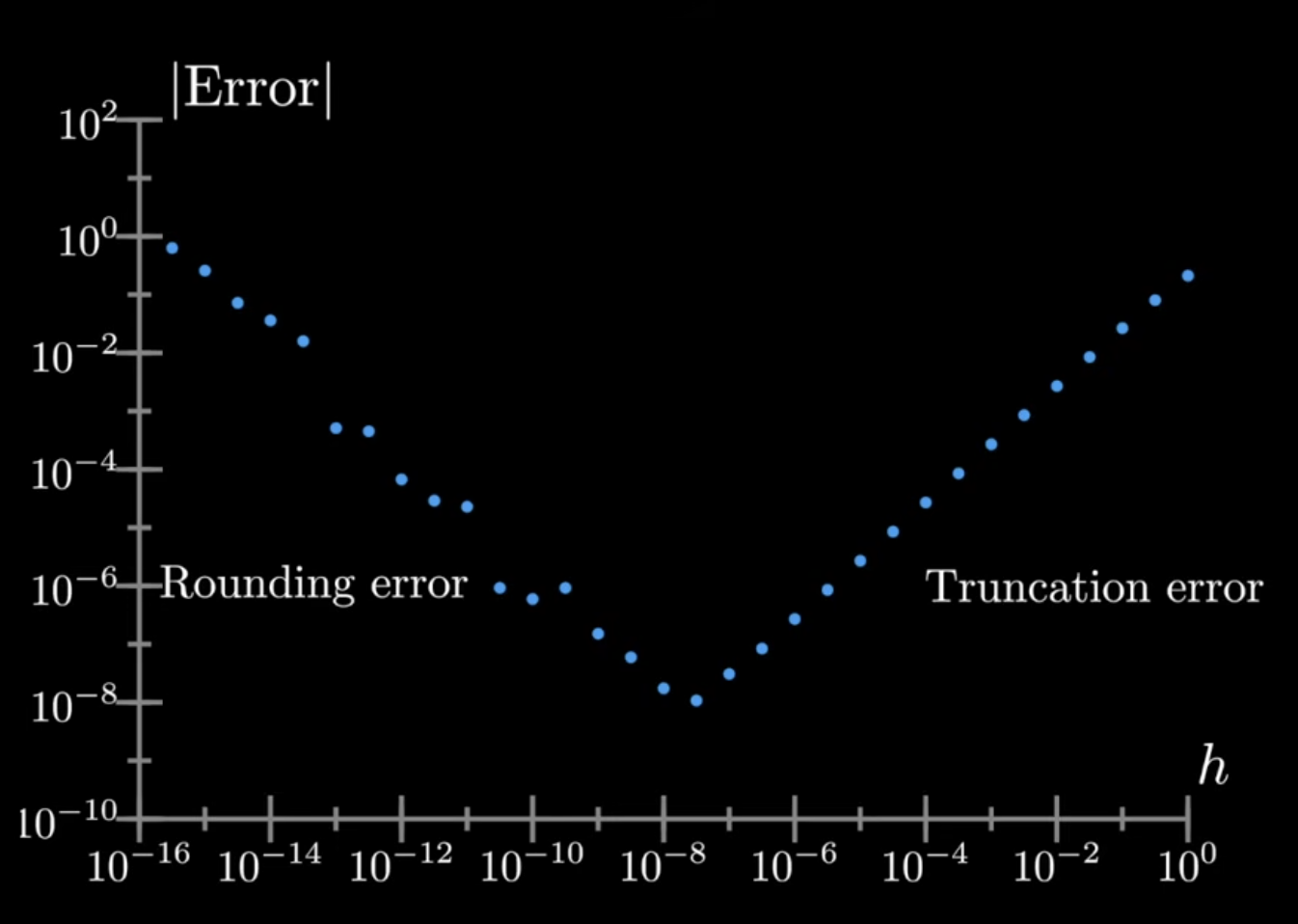
Machine Learning does not have an issue with rounding error, namely because precision is not the primary objective, as Gradient Descent only uses a noisy estimation of the gradient.

The issue arises in the fact that this requires $O(n)$ evaluations which is a time Complexity that scales poorly for millions of parameters.

$$e_1,e_2,e_3,\dots ,e_n$$

Symbolic Evaluation