Graphs

I am sure we are all familiar with graphs, given that this whole note repo is graph-based! But in computer science, graphs are a fundamental data structure used to model relationships between entities. They consist of vertices (or nodes) and edges (connections between nodes).

This will deal with defining graphs formally, and some common algorithms that operate on them.

---

Undirected Graphs

Undirected graphs are defined as:

$$G=(V,E)$$

where:

• $V$ is the set of vertices (or nodes).
• $E$ is the set of edges, which are unordered pairs of vertices. An edge
• Captures a bidirectional relationship between two vertices.
• Graph size parameters:
  • $|V|=n$ (number of vertices)
  • $|E|=m$ (number of edges)

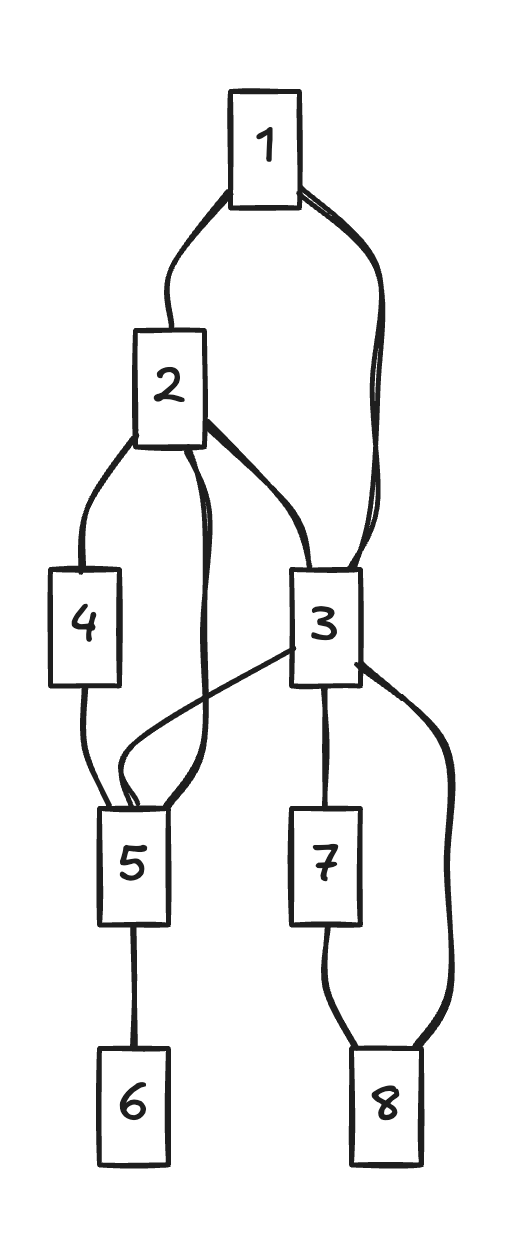
Example

Say we define a graph with the following parameters:

$$\begin{array}{rl}V& =\{1,2,3,4,5,6,7,8\}\\ E& =\{(1,2),(1,3),(2,3),(2,4),(2,5),(3,5),(3,7),(3,8),(4,5),(5,6),(7,8)\}\\ n& =8\\ m& =11\end{array}$$

This would yield a graph looking like:

Question

What is the minimum and maximum numbers of edges in an undirected graph with $n$ vertices?

Answer

The minimum number of edges is $0$ (an empty graph), and the maximum number of edges is $\frac{n(n-1)}{2}$ (a complete graph where every pair of vertices is connected by an edge).

---

Directed Graphs

Similarly, directed graphs are defined as:

$$G=(V,E)$$

Where:

• $V$ is the set of vertices (or nodes).
• $E$ is the set of edges between ordered pairs of vertices.
• Captures pairwise relationships between two vertices, but in a specific direction (from one vertex to another).
• Graph size parameters:
  • $|V|=n$ (number of vertices)
  • $|E|=m$ (number of edges)

Returning to the Example

Going back to the same definition from before, lets see what happens when we construct a directed graph from the same parameters:

$$\begin{array}{rl}V& =\{1,2,3,4,5,6,7,8\}\\ E& =\{(1,2),(1,3),(2,3),(2,4),(2,5),(3,5),(3,7),(3,8),(4,5),(5,6),(7,8)\}\\ n& =8\\ m& =11\end{array}$$

We get:

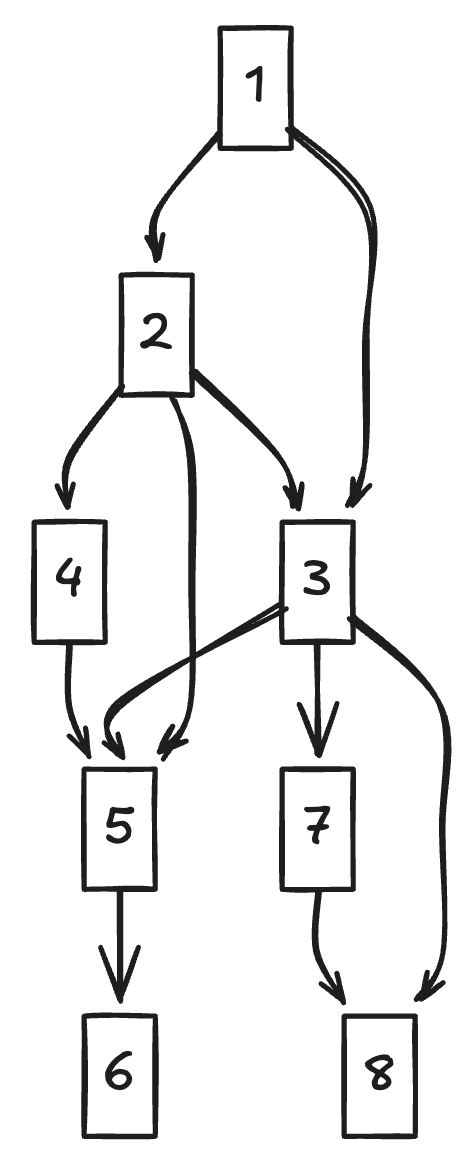
Looks quite similar! But with one obvious change.

Question

What is the minimum and maximum numbers of edges in a directed graph with $n$ vertices?

Answer

The minimum number of edges is $0$ (an empty graph), and the maximum number of edges is $n(n-1)$ (a complete directed graph where every pair of vertices is connected by a directed edge in both directions).

---

Alternative Representation

Graphs can be represented in various ways, and one common method is using an Adjacency Matrix. An adjacency matrix is a 2D array where the rows and columns represent the vertices of the graph, and the entries indicate whether there is an edge between the vertices.

Another way to represent them is with an Adjacency List. Like the adjacency matrix, it represents which vertices are connected to which other vertices, but does so in a more space-efficient manner for sparse graphs.

Comparing Complexity of the Two

Complexity	Adjacency Matrix	Adjacency List
Storage space	$\Theta (n^2)$	$\Theta (m+n)$
Check edge$(u,v)$	$\Theta (1)$	$O(n)$
Find all edges	$\Theta (n^2)$	$\Theta (m+n)$

Side note:

• As a graph becomes dense, $\Theta (m+n)$ approaches $\Theta (n^2)$ because $m$ approaches $\Theta (n^2)$
• As a graph becomes sparse, $\Theta (m+n)$ approaches $\Theta (n)$ because approaches $\Theta (n)$