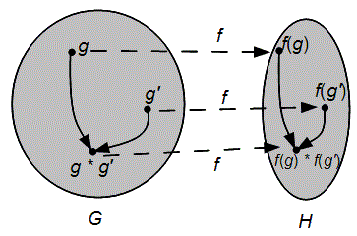
An Isomorphism, in the context of group theory, is a bijective Homomorphism between two groups. This means that there exists a one-to-one correspondence between the elements of the two groups that preserves the group operation.
A very simple example for those not familiar with group theory would be the Isomorphism between the ways you can arange 4 dots in a line, and the ways you can rotate a cube. Both have 24 different arrangements, and the way you can go from one arrangement to another is the same in both cases.
An Isomoprhism in this case indicates that applying two transformations in sequence will yield a single transformation in that set, and that this is true for both sets of transformations.