A Bijection simply refers to a function that is both injective (one-to-one) and surjective (onto). In laymann’s terms, it serves as a mapping between two sets where each element in the first set corresponds to exactly one unique element in the second set, and vice versa. This means that every element in both sets is paired with exactly one element from the other set, ensuring a perfect “one-to-one correspondence” between the two sets.
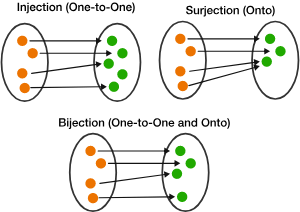
Think of the Pigeonhole Principle, and how if you have more pigeons than pigeonholes, at least one pigeonhole must contain more than one pigeon. A bijection avoids this by ensuring that each pigeon (element from the first set) has its own unique pigeonhole (element from the second set), and every pigeonhole is filled (every element in the second set is paired with an element from the first set).
Another example from Cardinality can be seen in mapping , where each natural number is paired with its double. This is a bijection because every natural number has a unique double, and every even number (element of ) corresponds to exactly one natural number.