Jensen's Inequality

Probably one of the most fundamental building blocks to fields like Information Theory and later Variational Inference. In laymans terms, it states that for Convex Function, the function of the average is less than or equal to the average of the function. This has deep implications in understanding expectations and variances in probabilistic systems.

---

Formal Definition

1. Linear Edition

If $f$ is convex (shaped like a smile $\cup$), then for any two points $x,y$ in the domain of $f$, and a weight $0\le \theta \le 1$:

$$f(\theta x+(1-\theta )y)\le \theta f(x)+(1-\theta )f(y)$$

Imagine drawing a straight line connecting two points on a curved “smiley face” graph. For a convex shape, the straight line connecting two points always sits above the curve itself. The weighted average of the function values is greater than the function of the weighted average.

• Right Side: The straight line (the chord).
• Left Side: The actual curved function.

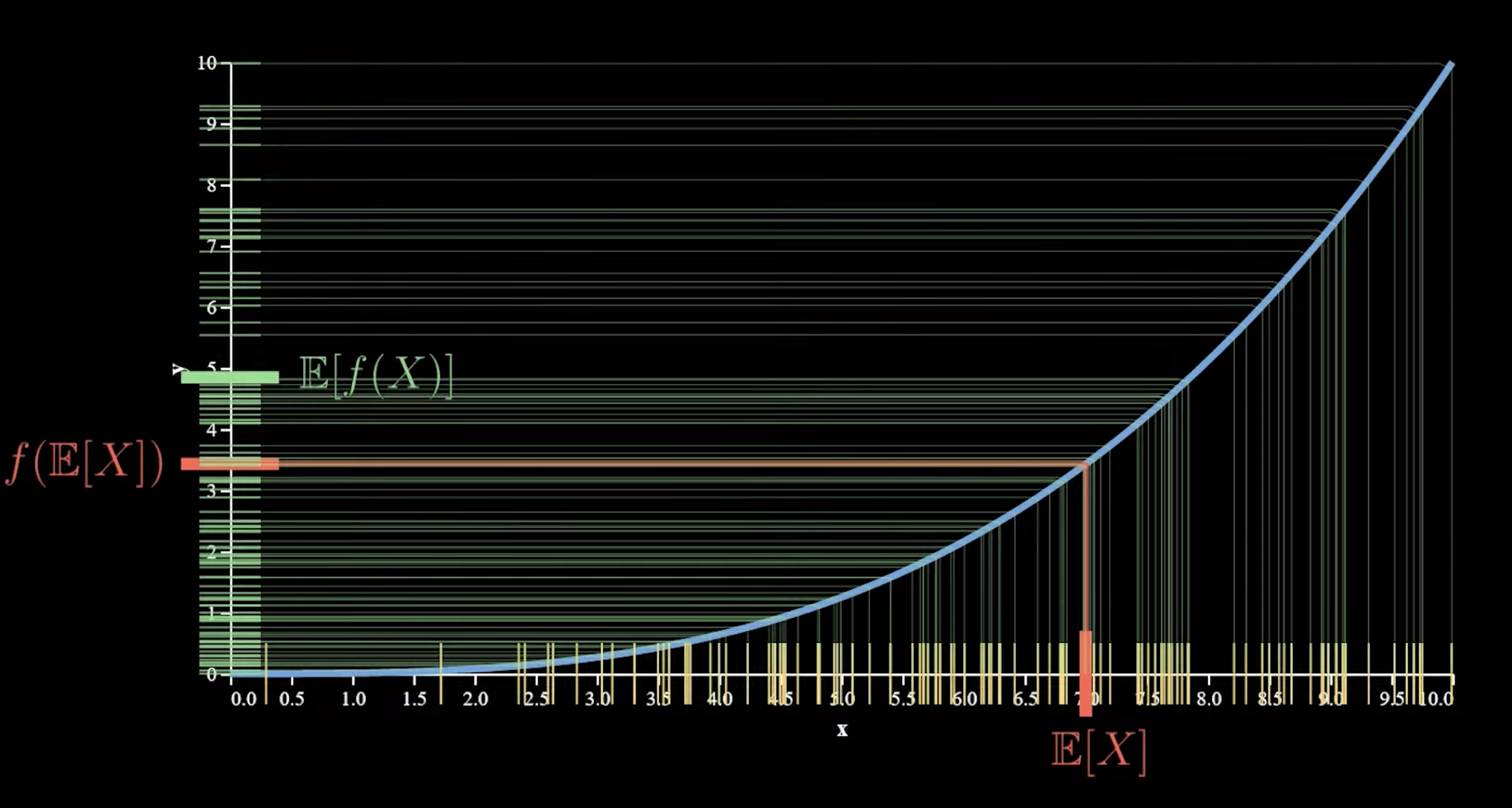
2. Probabilistic Extension

Let $f$ be a convex function (where the slope is increasing, i.e., $f^{\prime \prime }(x)\ge 0$) and let $x$ be a random variable. Then:

$$f(\mathbb{E}[x])\le \mathbb{E}[f(x)]$$

Equality Condition:

If $f$ is strictly convex ($f^{\prime \prime }(x)>0$), then equality, $\mathbb{E}[f(x)]=f(\mathbb{E}[x])$, holds if and only if $x$ is a constant (no variance).

If a system is convex (like compound interest or options), adding volatility (randomness) actually increases the expected outcome. Being exposed to the ups and downs (the average of the function) is better than staying at the steady average (the function of the average).

• Left Side: The Function of the Average.
• Right Side: The Average of the Function.

3. The Basic Case

This connects the Linear Edition to the Probabilistic Edition. If we treat the weight $\theta$ as a probability:

$$P(z=x)=\theta ,P(z=y)=1-\theta$$

The “Linear Edition” is just a specific example of the “Probabilistic Extension” where your random variable only has two possible outcomes ($x$ or $y$). It proves that the logic holds for simple weighted averages just as it does for complex probability distributions.

4. Concave Edition

Let $f$ be a concave function (shaped like a frown $\cap$, i.e., $f^{\prime \prime }(x)\le 0$) and let $x$ be a random variable. Then:

$$f(\mathbb{E}[x])\ge \mathbb{E}[f(x)]$$

Equality Condition:

If $f$ is strictly concave ($f^{\prime \prime }(x)<0$), then equality holds if and only if $x$ is a constant.

This is the logic of diminishing returns (like the utility of money). In a concave world, reliability is valuable. The “average of the outcomes” is usually worse than the “outcome of the average.” The straight line sits below the curve.

• Scenario: Would you rather have a guaranteed $50(FunctionoftheAverage),ora50/50coinflipfor$0 or $100 (Average of the Function)?
• Result: Most people prefer the guaranteed $50.