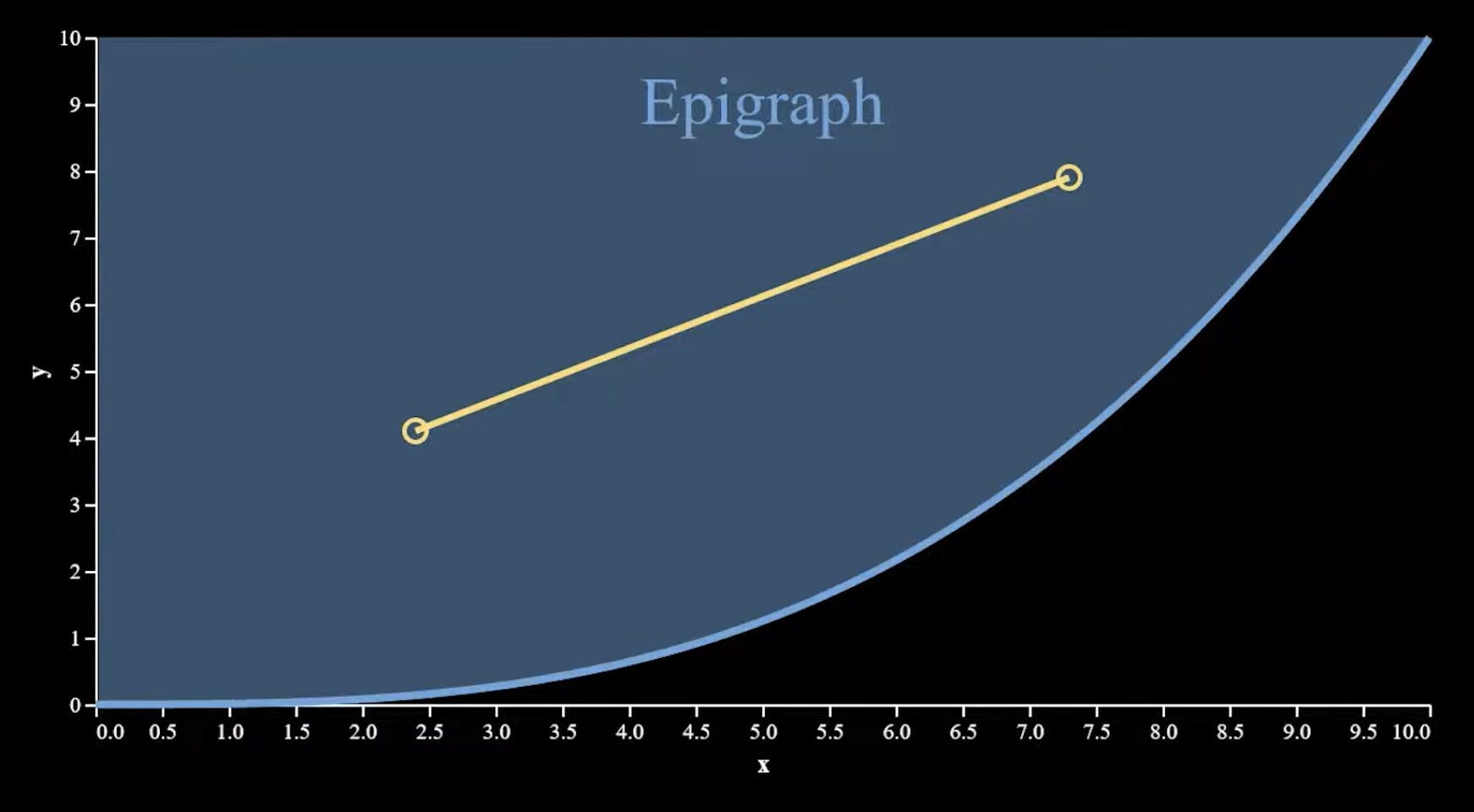
A lot simpler than it sounds, all a convex function is, is a function where a line segment connecting any two points on the graph of the function lies above or on the graph. In other words, if you pick any two points on the curve and draw a straight line between them, that line will never dip below the curve itself.
We call this area the epigraph of the function, think of the opposite side of what we usually try to find when integrating a function.
Thinks like and are convex functions, while a normal distribution’s bell curve is not. If you can find two points in the epigraph space that dip there, it is not convex.