The Ising Model serves as a simplified mathematical framework to understand phase transitions and critical phenomena in statistical mechanics. It consists of discrete variables called “spins” that can take on one of two values, typically represented as +1 or -1. These spins are arranged on a lattice, where each spin interacts with its nearest neighbors.
These “spin” values are both influenced by their nearest neighbors and an external magnetic field. The model captures the competition between thermal agitation, which tends to randomize the spins, and the interaction energy, which tends to align them. The important idea to note is the tendancy for system to “fall” to the lowest energy state possible.
The Ising Model is also what inspired John Hopfield to create Hopfield Networks, the precursor to modern Neural Networks. These would mimic the Ising Model in that it could use this energy minimization to “remember” patterns.
However, its applicability extends beyond magnetism and physics itself. The Ising Model introduced the idea of a “critical point,” a concept that has been influential in computational neuroscience, where neuronal avalanches exhibit similar phase transition behavior. Good example from paper Neuronal Avalanches in Neocortical Circuits - PMC
The characteristics of this “critical point” are that the “patterns” we see are scale-invariant, meaning they look similar regardless of the scale at which we observe them. This property is crucial in understanding complex systems, as it suggests that the same underlying principles govern behavior across different scales.
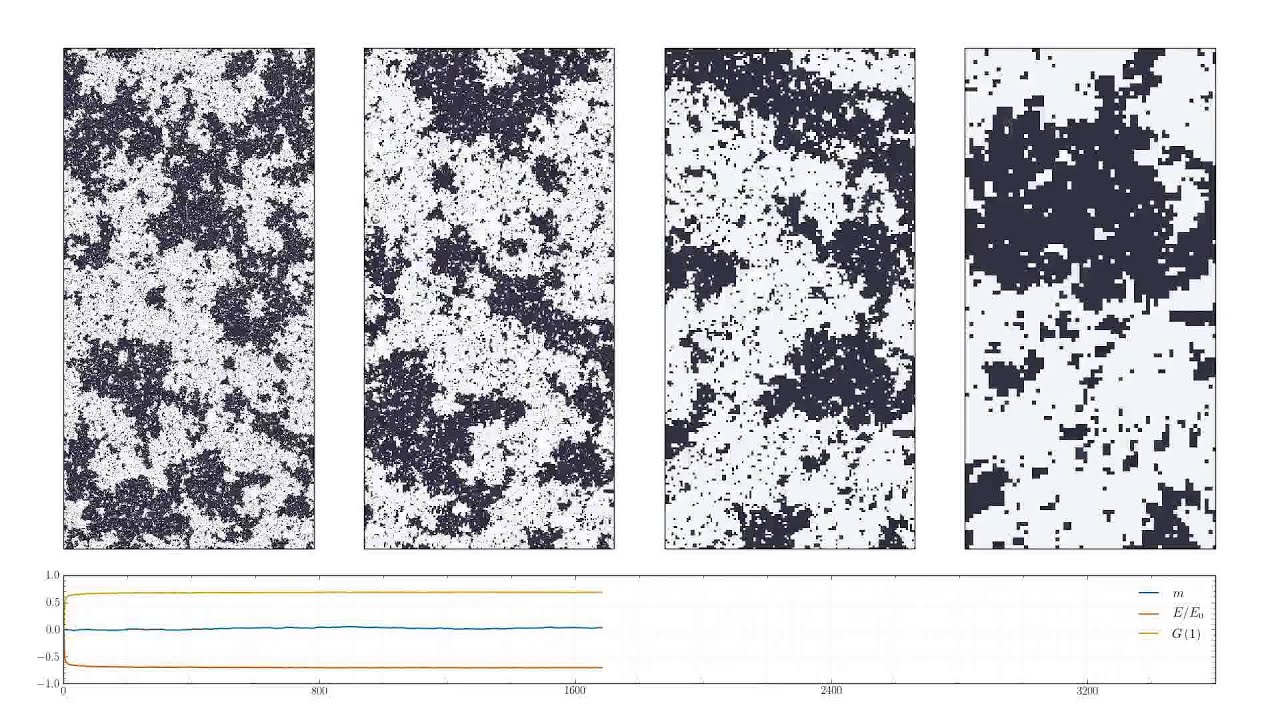
Formulation
We can mathematically express the Ising Model using the Hamiltonian function, which represents the total energy of the system:
Where:
- is the Hamiltonian (total energy) of the system.
- is the interaction strength between neighboring spins.
- and are the spin variables at sites