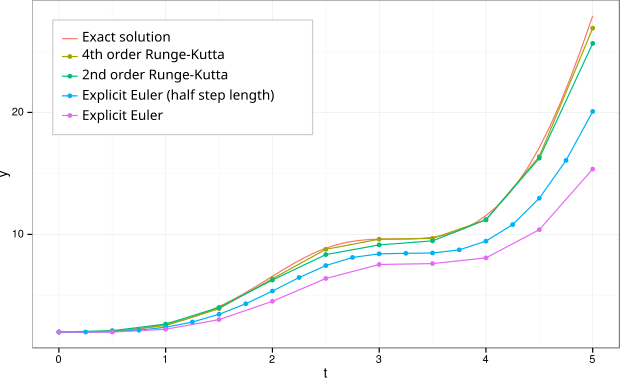
Runge Kutta

Runge Kutta is a Ordinary Differential Equation approximation method known for its accuracy to efficiency ratio. It is a type of single-step method, meaning it only uses information from the current point to estimate the next point, rather than relying on multiple previous points.

It is a much better approximation method than Eulers Method, as it uses multiple evaluations of the derivative within each step to achieve higher accuracy.

Forms and Formula

The general Runge Kutta formula can be defined as:

$$y_{n+1}=y_n+h\sum _{i=1}^s{b}_i{k}_i$$

where the slopes are:

$$k_i=f\left(t_n+c_{i}h,y_n+h\sum _{j=1}^s{a}_{ij}{k}_j\right)$$

There are two popular forms of Runge Kutta, namely $R{K}_4$ and $R{K}_2$.

RK4

$$\begin{array}{rl}{k}_1& =f(t_n,y_n)\\ k_2& =f(t_n+\frac{h}{2},y_n+\frac{h}{2}{k}_1)\\ k_3& =f(t_n+\frac{h}{2},y_n+\frac{h}{2}{k}_2)\\ k_4& =f(t_n+h,y_n+h{k}_3)\\ y_{n+1}& =y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\end{array}$$

RK2

$$\begin{array}{rl}{k}_1& =f(t_n,y_n)\\ k_2& =f(t_n+\frac{h}{2},y_n+\frac{h}{2}{k}_1)\\ y_{n+1}& =y_n+h{k}_2\end{array}$$