Dynamical Systems Theory is the study of systems that evolve over time according to a set of rules. It is a branch of mathematics that deals with the behavior of complex systems and how they change over time.
While Differential equations are at the heart of Dynamical Systems Theory, the field encompasses a broader range of concepts and tools.
One example would be the interest in high dimensional manifolds and their properties, which can be studied using techniques from topology and geometry.
For Computational Neuroscience, Dynamical Systems Theory is particularly relevant because it provides a framework for understanding how neural systems evolve over time and how they respond to external stimuli. And, at least for Grid Cells, they can be mapped to manifolds like a Torus.

These kind of manfiold embeddings only emerge because we have paired many different state variables as dimensions in a high dimensional space. This is a common technique in Dynamical Systems Theory, where we often study the behavior of systems in high-dimensional spaces. Then, we can get a visual understanding of the system’s behavior by projecting it onto a lower-dimensional space using techniques like UMAP.
Semantic Shorthands
Because Differential Equations for Dynamical Systems are almost always stepping with respect to time, we use newtonian shorthand of , assuming that we are taking the derivative of with respect to :
Becomes:
These are called Autonomous Differential Equations
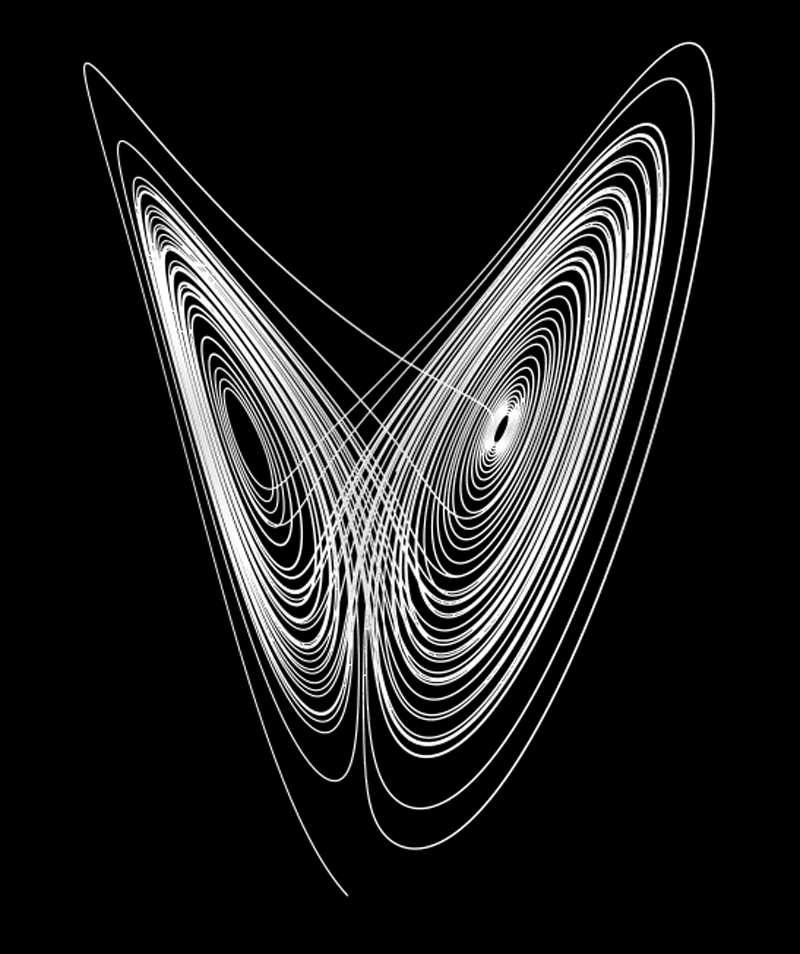
Attractors
Attractor serve as a way to summarize the long-term behavior of a dynamical system. They represent the states or sets of states that the system tends to evolve towards over time, regardless of its initial conditions.
The most well known is the Lorenz Attractor, which arises from a simplified model of atmospheric convection. It is defined by the following set of differential equations: