Eulers Formula

for a Welch Labs video

There is a really beautiful concept in the world of Mathematics that the fundamental equations and functions on the $xy$ plane are just a small part of a more elegant, complete picture of higher dimensional mathematics.

This has everything to do with the imaginary number $i$ and the idea of the complex number plane. I like to think this is more than common mathematical knowledge now, but the steps in which this plane was discovered is a beautiful path on its own.

When you extend polynomials such as $f(x)=x^2+1$ to include the imaginary number plane $x=a+bi$ is a relatively simple process. However, there exists one pair of functions ( exponentials and logarithms ), where the application of imaginary numbers isn’t immediately clear.

---

The straightforward rule of exponents is that the power dictates how many times you multiply the base by itself:

$$2^3=2\cdot 2\cdot 2$$

But how can you apply this fundamental rule to non-standard cases like $\sqrt{-1}$? What does it mean to raise $2$ to the power of $\sqrt{-1}$?

$$2^{\sqrt{-1}}=?$$

This was the subject of deep debate during the early 1700s, which posed a very real threat to the still very new foundations of mathematical analysis. This was brought to an end when Leonhard Euler came up with a solution so elegant, it has garnered a reputation as the most beautiful equation in mathematics.

---

The Log Debate

This began when Gottfried Wilhelm Leibniz sent a letter to fellow mathematician Johann Bernoulli, claiming it was impossible to take the log of a negative number.

Leibniz would later detail in another letter to Bernoulli that logs are just another way to write exponents, and would simply not make sense when applied to negatives.

starting here, we will construct a table of exponentials and their equivalent logarithms, and the work used to do so.

A $\log$ of base $2$ of $8$ yields $3$, because taking the $3rd$ power of $2$ is $8$.

Example Exponential	Equivelant Logarithm	Work
$2^3=8$	${\log }_2(8)=3$	$2^3=2\cdot 2\cdot 2=8$

A slightly weirder case would be that of $2^0$, which is known to be $1$. ${\log }_2(1)$ is $0$, which makes sense assuming that $2^0=1$.

The reason $2^0$ is $1$ and not something else, is that this definition preserves an important rule and property of exponents/logs. It is understood that when you multiply two terms with the same base but different exponents, you add the exponents.

$$\begin{array}{rl}{2}^a\cdot 2^b& =2^{a+b}\\ 2^3\cdot 2^3& =(2\cdot 2)(2\cdot 2\cdot 2)=2^5\end{array}$$

By defining $2^0$ as $1$ we preserve this rule, $2^{3+0}$ should equal $2^3$ and $2^3\cdot 2^0$.

Example Exponential	Equivelant Logarithm	Work	Reasoning
$2^3=8$	${\log }_2(8)=3$	$2^3=2\cdot 2\cdot 2=8$	Definition of raising to a power
$2^0=1$	${\log }_2(1)=0$	$2^{3+0}=2^3=2^3\cdot 2^0$	\begin{align*} 2^{a} \cdot 2^{b} &= 2^{a+b} \\ 2^3 \cdot 2^3 &= (2 \cdot 2) (2 \cdot 2 \cdot 2) = 2^5 \end{align*}

We are taking the approach of finding mathematical consistency between the various exponential and logarithmic equivalents, so as to truly gain an appreciation for the elegance of Euler’s approach.

Another relatively straightforward equivalency is that of logarithms of fractions between $0$ and $1$. Just as multiplying exponentials leads to their powers being added together, division is equivalent to just subtracting the exponents.

For this reason, it means that $2^{-2}$ on its own must equal $\frac{1}{2^2}$, and thus $\frac{1}{4}$. This is how we arrive at the logarithms of fractions.

Example Exponential	Equivelant Logarithm	Work	Reasoning
$2^3=8$	${\log }_2(8)=3$	$2^3=2\cdot 2\cdot 2=8$	Definition of raising to a power
$2^0=1$	${\log }_2(1)=0$	$2^{3+0}=2^3=2^3\cdot 2^0$	\begin{align*} 2^{a} \cdot 2^{b} &= 2^{a+b} \\ 2^3 \cdot 2^3 &= (2 \cdot 2) (2 \cdot 2 \cdot 2) = 2^5 \end{align*}
$2^{-2}=\frac{1}{2^2}=\frac{1}{4}$	${\log }_2\left(\frac{1}{4}=-2\right)$	$\frac{2\cdot 2\cdot 2}{2\cdot 2}=\frac{2^3}{2^2}=2^{3-2}=2^3\cdot 2^{-2}=2$ $\to 2^{-2}=\frac{1}{2^2}=\frac{1}{4}$	Preserves Property $\frac{2^a}{2^b}=2^{a-b}$

Now, we are finally confronted with the problem of logarithms of negatives. As Leibniz claimed, we have essentially run out of options. What possible power of 2 could result in $-1$? Neither positive or negative numbers will work in this case. In a response letter Bernoulli flatly rejected this claim, arguing that since the derivatives of $\log (x)$ and $\log (-x)$ both evaluate to $\frac{1}{x}$, this must mean that both $\log (x)$ and $\log (-x)$ are equal:

$$\begin{array}{rl}\frac{d}{dx}& \log (x)=\frac{1}{x}\\ \frac{d}{dx}& \log (-x)=\frac{1}{-x}=\frac{1}{x}\\ \to & \log (x)=\log (-x)\end{array}$$

This would lead to the conclusion that the $\log$ function didnt just have a single curve, and instead had both a positive and negative branch, symmetric of each other.

This is the equivalent of supplying the absolute value of $x$ to the $\log$ function

Desmos

Leibniz was not convinced of this property, and the two mathematicians would go back and forth for over a year discussing this issue.

Euler later noted when picking up this problem that not finding a solution would leave an indelible stain in analysis. In fact, if this problem was not to be solved, it would leave a fundamental flaw in the field of calculus, a young and delicate field at the time. For this very reason, many mathematicians at the time were believed to withhold publishing proofs at the time.

As an answer to this gaping hole in Calculus, Euler published a beautifully elegant 13-page paper, where he pointed out logical flaws in both the solutions provided by Leibniz and Bernoulli, while simultaneously providing a solution of his own.

Regarding Bernoulli’s Theory

Euler demolishes Bernoulli’s theory that $\log (x)=\log (-x)$. Euler argued that just because $\log (x)$ and $\log (-x)$ have the same derivative, this doesn’t guarantee that the functions themselves are equal:

$$\begin{array}{rl}\frac{d}{dx}\log (x)& =\frac{1}{x}\\ \frac{d}{dx}\log (-x)& =-\frac{1}{-x}=\frac{1}{x}\\ & \to \log (x)=\log (-x)\end{array}$$

This is the case because the same faulty logic can be used to prove that $\log (2x)=\log (x)$, a clearly impossible statement:

$$\begin{array}{rl}\frac{d}{dx}\log (x)& =\frac{1}{x}\\ \frac{d}{dx}\log (2x)& =2\cdot \frac{1}{2x}=\frac{1}{x}\\ & \to \log (x)=\log (2x)\end{array}$$

Regarding Leibniz’s Theory

Here, Euler draws from one of Bernoulli’s own examples to show that Leibniz was partially correct:

Bernoulli, while investigating finding the areas of circle sectors, got stuck on this difficult integral that computes the area of a sector, as a function of the position $x,y$ on the corner of the sector:

$$AREA=\int \sqrt{a^2-x^2}dx$$

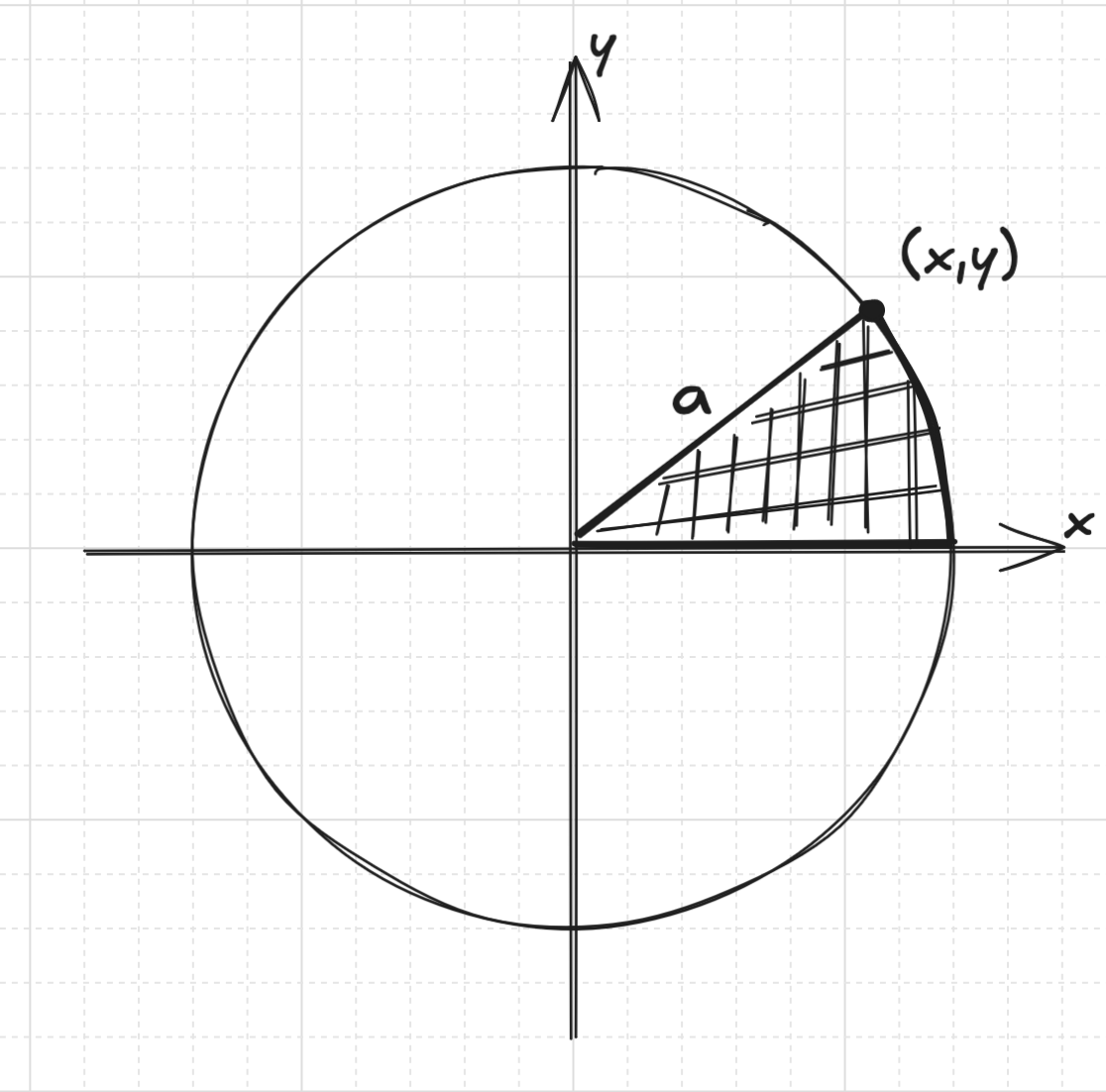
Bernoulli realized that if he effectively pulled a square root of $-1$ out of his expression, he was able to evaluate the integral:

$$=\frac{a^2}{4i}\log \frac{x+yi}{x-yi}$$

The result is quite a complex expression for the area of the sector, involving $i$ and a logarithm. Euler showed that if you chose the point $x,y$ to be $(0,1)$, Bernoulli’s equation would simplify, into the logarithm of $-1$ over $4i$:

$$AREA=\frac{1}{4i}\log \left(\frac{-i}{i}\right)=\frac{1}{4i}\log (-1)=\frac{\log (-1)}{4i}$$

He argued that since the area of the sector was clearly a real quantity, that the $i$ in the denominator would have to cancel with the $i$ in the numerator.

This meant that the $\log (-1)$ would have to be some “imaginary” number. However, it is not possible to just declare that a logarithm of a negative number is imaginary, and it doesn’t really fix the problem at hand, and in reality leads to its own new set of contradictions.

---

Namely, a key property of logarithms is that raising an argument of a logarithm to a certain power is equivalent to multiplying the logarithm by the power.

$$\begin{array}{r}\text{POWER IDENTITY}\\ \log (x^N)=N\log (x)\\ {\log }_2(2^3)=3{\log }_2(2)\\ {\log }_2(8)=3\cdot 1\\ 3=3\end{array}$$