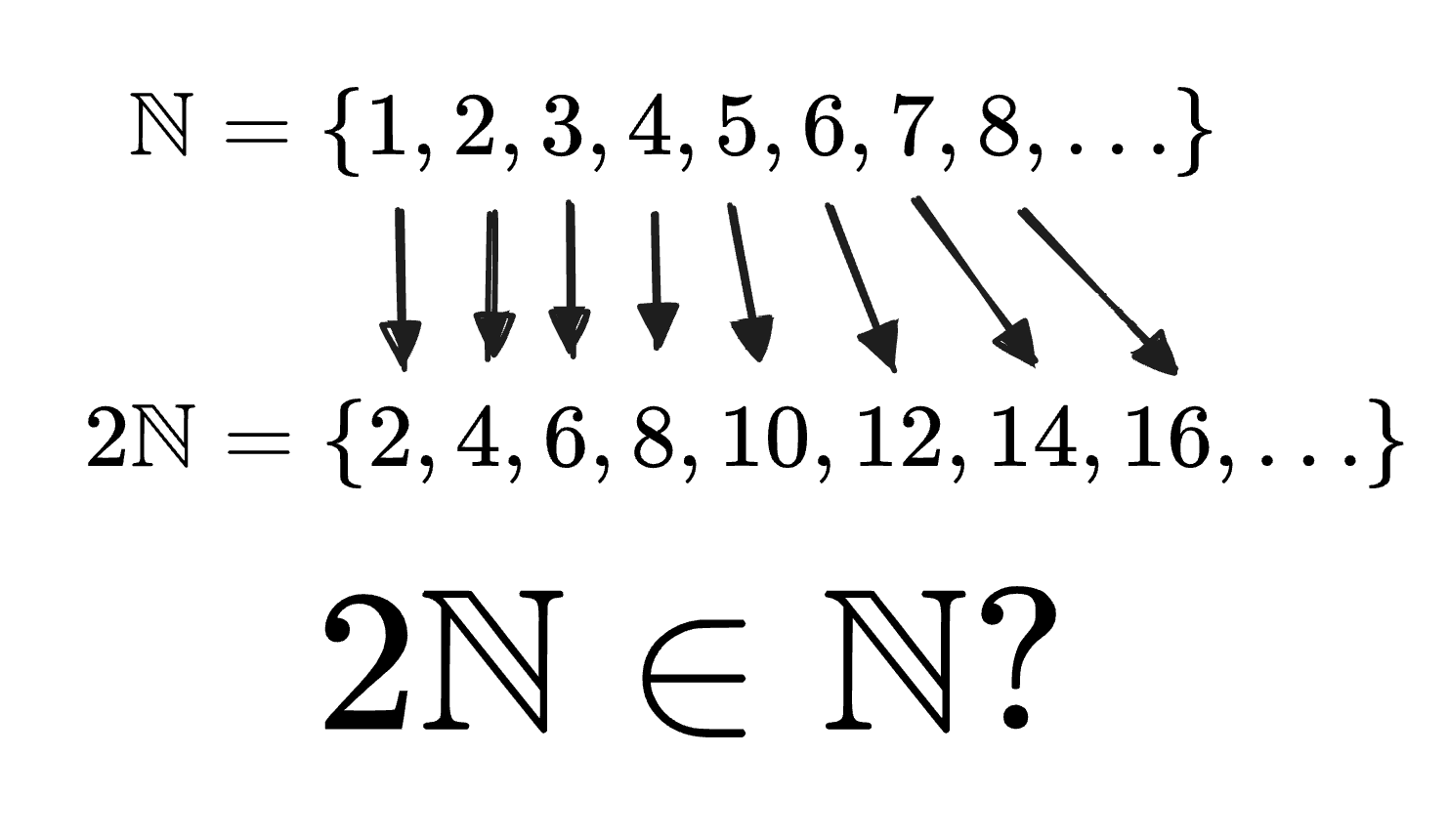Cardinality

In Layman’s terms, cardinality is a way to measure the “size” of a set, which can be finite or infinite.

For the case of finite sets, the cardinality is the exact number of elements in that set.

$$A=\{1,2,3\}⟹|A|=3$$

For infinite sets, cardinality helps us understand different “sizes” of infinity. For example, the set of natural numbers $\mathbb{N}=\{1,2,3,\dots \}$ has a cardinality denoted as ${\aleph }_0$ (Aleph Null), which represents the smallest infinity.

$$A=\{1,2,3,\dots \}⟹|A|={\aleph }_0$$

---

A fascinating aspect of infinite sets is that we can establish a one-to-one correspondence (bijection) between seemingly different infinite sets. For instance, consider mapping the natural numbers $\mathbb{N}=\{1,2,3,\dots \}$ to the set of even natural numbers $2\mathbb{N}=\{2,4,6,\dots \}$ using the function $f(n)=2n$. This mapping shows that both sets have the same cardinality ${\aleph }_0$, even though $2\mathbb{N}$ appears to be a “proper subset” of $\mathbb{N}$. This counterintuitive result illustrates how our finite intuitions break down with infinite sets, leading to complications like Hilbert’s Hotel paradox, where properties that seem obvious for finite collections no longer hold when dealing with infinite quantities.