Cross Validation is the primary statistical method used to estimate the skill of machine learning models. It is used to protect against overfitting in a predictive model, particularly in a case where the amount of data may be limited.
Cross Validation Methods
Repeated Random Sub-sampling Validation

Also known as Monte Carlo cross-validation, this method involves randomly splitting the dataset into training and testing data multiple times. Each time, a model is trained on the training set and evaluated on the test set. The results are then averaged to provide an overall performance estimate.
This is a simple and effective method, but it can be computationally expensive, especially with large datasets or complex models.
K-Fold Cross Validation
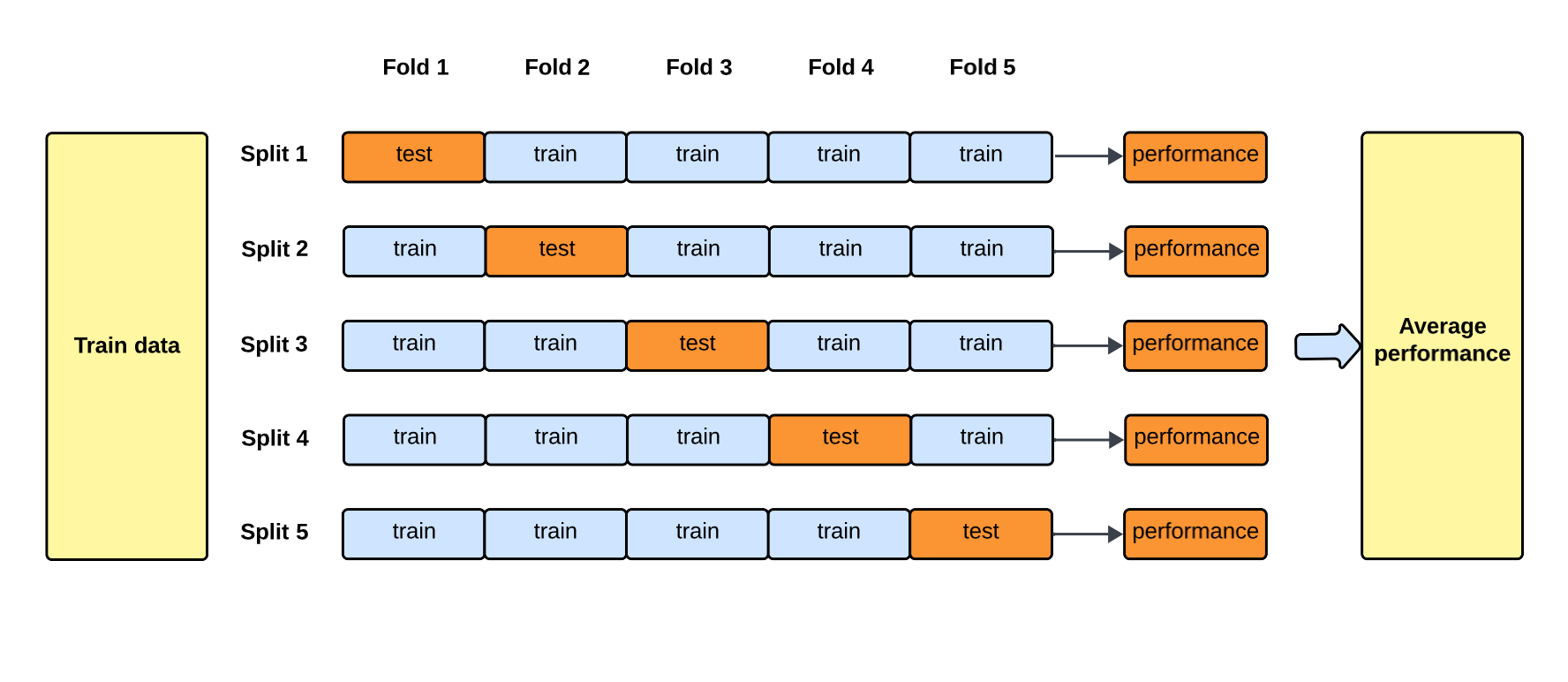
Splits the dataset into k equally sized folds. The model is trained k times, each time using a different fold as the test set and the remaining k-1 folds as the training set. The results are then averaged to provide an overall performance estimate.
Works well for most datasets and is less computationally expensive than repeated random sub-sampling validation.
Leave-One-Out Cross Validation
Special case of K-Fold Cross Validation where k is equal to the number of data points in the dataset. Each data point is used once as a test set while the remaining data points form the training set.
For a dataset with n data points, the model is trained n times. This method can be computationally expensive for large datasets but provides an unbiased estimate of model performance.
Upside is there is a lot of training data used for each model.
Grid Vs Random Search for Model Selection
When tuning the hyperparameters of an estimator, Grid Search and Random Search are two common methods used to find the best combination of hyperparameters.
Grid Search
Sets up a grid of hyperparameter values and evaluates the model for each combination. This method is exhaustive and guarantees that the best combination will be found, but it can be computationally expensive, especially when the number of hyperparameters is large.
Random Search
Randomly samples hyperparameter combinations from a specified distribution. This method is less computationally expensive than grid search and can often find good hyperparameter combinations more quickly, especially when only a few hyperparameters significantly impact model performance.
Process for Both
We generally:
- Loop over a set of hyperparameter combinations (either grid or random).
- Conduct cross-validation for each combination to evaluate model performance.
- Select the combination that yields the best cross-validation performance.
Bias Vs Variance
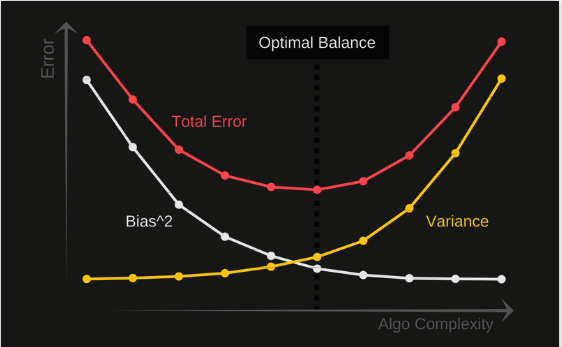
Analogous to the Uncertainty Principle, there is a trade-off between bias and variance in model performance. Fundamental law of nature, also visible in the Fourier Transform.
In this case, a model with high bias pays little attention to the training data and oversimplifies the model, leading to high error on both training and test data. A model with high variance pays too much attention to the training data and does not generalize well to unseen data, leading to low error on training data but high error on test data.
A learning curve plots your training/validation error against hte number of trianing examples. To plot it, run your algorithm using different training set sizes.
High Bias
If the algorithm is suffering from high bias, both the training and validation errors will be high. This indicates that the model is too simple to capture the underlying patterns in the data.