Homework 5

Problem 01

$E Q_{CFG} = {⟨ G, H ⟩ ∣ G,H are CFGs and L (G) = L H}$ . Show that $E Q_{CFG}$ is co-Turing recognizable.

To show that $E Q_{CFG}$ is recognizable, we will use the fact that:

we can decide if a word $w$ is in $L (G)$
we can list all strings $w$ as $Σ^{*}$ is enumerable

First we design a recognizer Turing machine $T$ :

Pseudocode:

I n p u t s : (G, H) \to {f or (i = {1, 2, ..}) \to {w_{i} = i o f Σ^{*} CFG m e mb ers hi p (G, w_{i}) \to {res u l t_{G}} CFG m e mb ers hi p (H, w_{i}) \to {res u l t_{H}} I F (res u l t_{G} \neq = res u l t_{H}) \to {A CCEPT}}}

If Turing machine $T$ accepts, then we have found a $w_{i}$ such that only one grammar generates it, meaning $L (G) \neq = L (H)$ .

If this is the case then there is at least a string for the symmetric difference. the language $Σ^{*}$ is fully exhausted, and thus the string must be some $w_{k}$ . Once it is reached, the two membership tests are in disagreement and thus the Turing machine accepts. And thus, $T$ halts for every input in the CFG $E Q_{CFG}$

In the other case where $L (G) = L (H)$ , this means that every string returns an identical membership answer, and the Turing machine will run forever as the if block is never reached.

And thus $T$ recognizes $E Q_{CFG}$ as required $■$

Problem 02

Let $A = {⟨ M ⟩ ∣ M is a DFA and M does not accept any string containing an even number of 0s}$ . Show that $A$ is a decidable language.

This is essentially the same as saying $L (M) \cap E = \emptyset$ , where $E = {w ∣ w contains even number of 0’s}$ .

Because these are both regular, we can make a DFA for the intersecction to test if that DFA has any reachable accept state given that we can decide on the emptiness of intersection.

We will make a new DFA for finding even number of 0’s, where $p_{0}$ is start and accept for when it has seen an even number of 0’s, and $p_{1}$ is otherwise.

Pseudocode:

I n p u t s : (M (df a)) \to {CONSRT U CT (D F A : P = M \times D_{e v e n}) \to {Q = {p_{0}, p_{1}} Σ = g i v e n q_{0} = {q_{0}, p_{0}} F = {p_{0}} δ = {(q, p), a} \to {δ (q, a), δ_{e v e n} (p, a)}} BFS (s t a r t p) \to {I F (a cce pt i s re a c hab l e) \to {re j ec t} e l se {a cce pt}}}

if this machine rejects, that means that an accepting state for the dfa $P$ is reachable, and therefore M does not accept string wtih even number of 0’s.

If this machine accepts, that means no accept state is reachable, and thus our claim $L (M) \cap E = \emptyset$ holds. M does not accept a string with an even number of 0’s.

Given that this is a DFA and there are only 2 states, the machine halts on every input.

Given that this turing machine decided the membership for all $A$ , the language is decidable $■$

Problem 03

Consider this Turing Machine ( adapted from Turing’s 1936 paper):

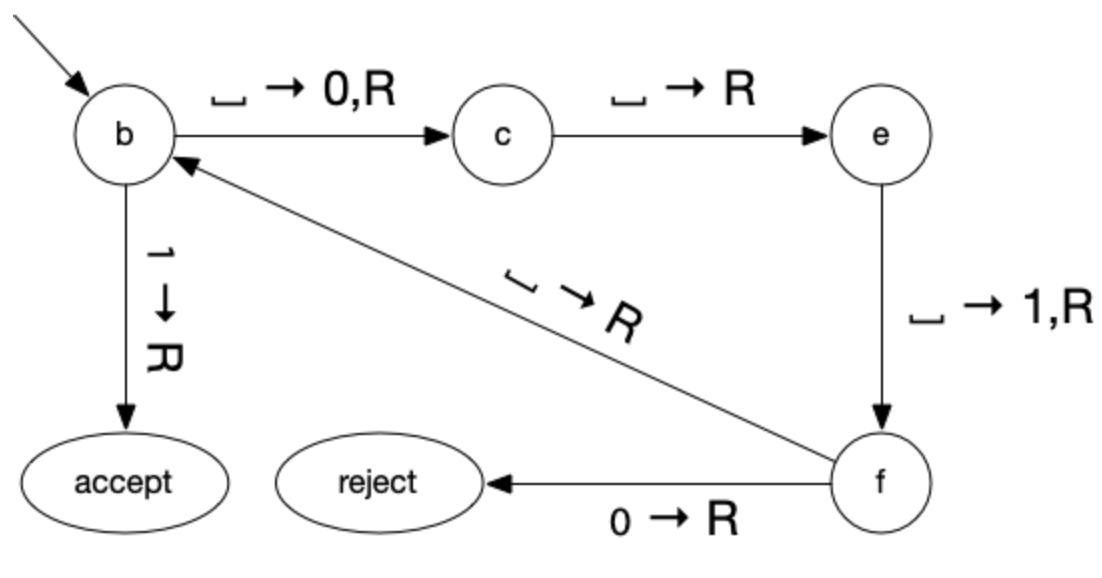
Assume for the following questions that this Turing Machine starts wtih an entirely blank tape.

Describe the behavior of this machine in plain English (but be precise!).
Will this machine ever halt? Why or why not?
Give the first five configurations of this machine.

Problem 04

Consider this context-free grammar:

\begin{align*} S &\to A | B \ A &\to 11A | B | \epsilon \ B &\to 11A | 0B | \epsilon \end{align*}

1. Describe the language of this CFG in plain English (but be precise!). Given a grammar $G=\{ w \in \{ 0,1 \}^{*} |\text{ every maximal block of consecutive 1's in w has an even length} \}$ This grammar is essentially meaning that there is no word in $L$ has a string of an odd number of consecutive ones, aka a single, triple, or 5 ones in a row. 2. Is this grammar ambiguous? If so, prove it. We know that a CFG is ambigious if a string has two seperate parse trees. This grammar is ambigous because there are many different parse trees, even for an empty word:

S \to A \to \epsilon

S \to B \to \epsilon

are both derivations for $\epsilon$, meaning they both have two different productions, and thus the parse trees are different. --- ## Problem 05 Consider this DFA: ![[Screenshot 2025-05-01 at 10.01.01 AM.png]] 1. Give a description of the language of this machine in set builder notation. 2. Give a complete formal definition of this machine, with complete specification of all elements in the tuple, including $\delta$. --- ## Problem 06 Consider this NFA: ![[Screenshot 2025-05-01 at 10.01.53 AM.png]] 1. Give a regular expression that describes the language of this machine. 2. Explain in plain English what occurs in this machine on input `001`. Be sure to account for all branches of computation. Draw a tree if it helps.

Graph View