Periodic Orbit Stability

(for the The Worldwide Air-Transportation Network website)

Chain Rule for Periodic Orbits

Chain rule for function composition: $(f \circ g)^{'} (x) = f^{'} (g (x)) \cdot g^{'} (x)$

When $f = g$ (composing a function with itself):

(f^{2})^{'} (x) = (f (f (x)))^{'}

( $f^{2}$ is f composed with f, not f squared, see Linear Systems)

Applying the chain rule:

(f^{2})^{'} (x) = f^{'} (f (x)) \cdot f^{'} (x)

Application to Period-2 Orbits

If ${p_{1}, p_{2}}$ is a period-2 orbit of $f$ , then:

$f (p_{1}) = p_{2}$ and $f (p_{2}) = p_{1}$
Equivalently: $f^{2} (p_{1}) = p_{1}$ and $f^{2} (p_{2}) = p_{2}$

Applying the chain rule to find the derivative at each point:

(f^{2})^{'} (p_{1}) = f^{'} (f (p_{1})) \cdot f^{'} (p_{1}) = f^{'} (p_{2}) \cdot f^{'} (p_{1})

Similarly:

(f^{2})^{'} (p_{2}) = f^{'} (f (p_{2})) \cdot f^{'} (p_{2}) = f^{'} (p_{1}) \cdot f^{'} (p_{2})

Key observation: Both derivatives are equal: $(f^{2})^{'} (p_{1}) = (f^{2})^{'} (p_{2}) = f^{'} (p_{1}) \cdot f^{'} (p_{2})$

This generalizes to any period- $n$ orbit. For a period-7 orbit, we compute:

(f^{7})^{'} (p_{i}) = f^{'} (p_{7}) \cdot f^{'} (p_{6}) \cdot \dots \cdot f^{'} (p_{1})

Stability of Periodic Orbits

Stability is a collective property of the entire orbit. All points in a periodic orbit share the same stability:

(f^{k})^{'} (p_{i}) = (f^{k})^{'} (p_{j}) \forall_{i, j}

for any periodic orbit ${p_{1}, p_{2}, \dots, p_{k}}$ .

In plain English, every point in a period- $k$ orbit has the same derivative when we apply $f^{k}$ , because they all cycle through the same sequence of local derivatives.

Definition: A periodic orbit ${p_{1}, p_{2}, \dots, p_{k}}$ is a sink (attracting) if $∣ f^{'} (p_{k}) \cdot f^{'} (p_{k - 1}) \cdot \dots \cdot f^{'} (p_{1}) ∣ < 1$

The orbit is a source (repelling) if the product has absolute value greater than 1.

Higher-Order Compositions

As you take higher compositions ( $f^{3}, f^{4}, f^{7}, \dots$ ), the pattern continues:

For $f^{n}$ , the fixed points include:

All original fixed points of $f$
All period-2 orbits (if $n$ is even, or any multiple of 2)
All period-3 orbits (if $n$ is a multiple of 3)
Generally, all period- $k$ orbits where $k$ divides $n$

Example: The graph of $f^{6}$ will intersect $y = x$ at points corresponding to:

Period-1 orbits (original fixed points)
Period-2 orbits ( $6 = 2 \times 3$ )
Period-3 orbits ( $6 = 3 \times 2$ )
Period-6 orbits

Each higher composition reveals more structure, turning periodic orbits into fixed points that can be analyzed using the chain rule.

Cobweb Plot Generator

Used claude to generate a little tool, mess around with parameter values to see what happens

Python

import numpy as np
import matplotlib.pyplot as plt

# ============ PARAMETERS ============
r = 3.5              # Logistic map parameter (0 < r <= 4)
x0 = 0.4             # Initial condition (0 < x0 < 1)
n_iterations = 50    # Number of iterations to plot
composition_order = 2  # Order of composition (1 = f, 2 = f^2, etc.)
# ====================================

def logistic_map(x, r):
    return r * x * (1 - x)

def composed_map(x, r, n):
    result = x
    for _ in range(n):
        result = logistic_map(result, r)
    return result

x_vals = np.linspace(0, 1, 1000)
y_vals = np.array([composed_map(x, r, composition_order) for x in x_vals])
x_cobweb = [x0]
y_cobweb = [0]

for i in range(n_iterations):
    x_cobweb.append(x_cobweb[-1])
    y_cobweb.append(composed_map(x_cobweb[-1], r, composition_order))

    x_cobweb.append(y_cobweb[-1])
    y_cobweb.append(y_cobweb[-1])

fig, ax = plt.subplots(figsize=(10, 10))
ax.plot([0, 1], [0, 1], 'k--', linewidth=1, label='y = x')
order_label = f'f(x)' if composition_order == 1 else f'f^{composition_order}(x)'
ax.plot(x_vals, y_vals, 'b-', linewidth=2,
        label=f'{order_label}, r = {r}')

ax.plot(x_cobweb, y_cobweb, 'r-', linewidth=0.5, alpha=0.7)
ax.plot(x0, 0, 'go', markersize=8, label=f'Start: x₀ = {x0}')

ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xlabel('x', fontsize=12)
ax.set_ylabel(order_label, fontsize=12)
ax.set_title(f'Cobweb Plot: Logistic Map ({order_label})', fontsize=14)
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_aspect('equal')

plt.tight_layout()
plt.show()

Output

Try these parameter combinations:

r = 2.8, composition_order = 1: Converges to fixed point
r = 3.2, composition_order = 1: Period-2 orbit (oscillates)
r = 3.2, composition_order = 2: Period-2 becomes fixed points
r = 3.5, composition_order = 1: Period-4 orbit
r = 4.0, composition_order = 1: Chaotic behavior

Logistic Map Bifurcations

We talked about this on day 1, but we didnt discuss the bifurcation diagram in detail.

Have a look at the interactive code block in the Logistic Map note, it should look something like:

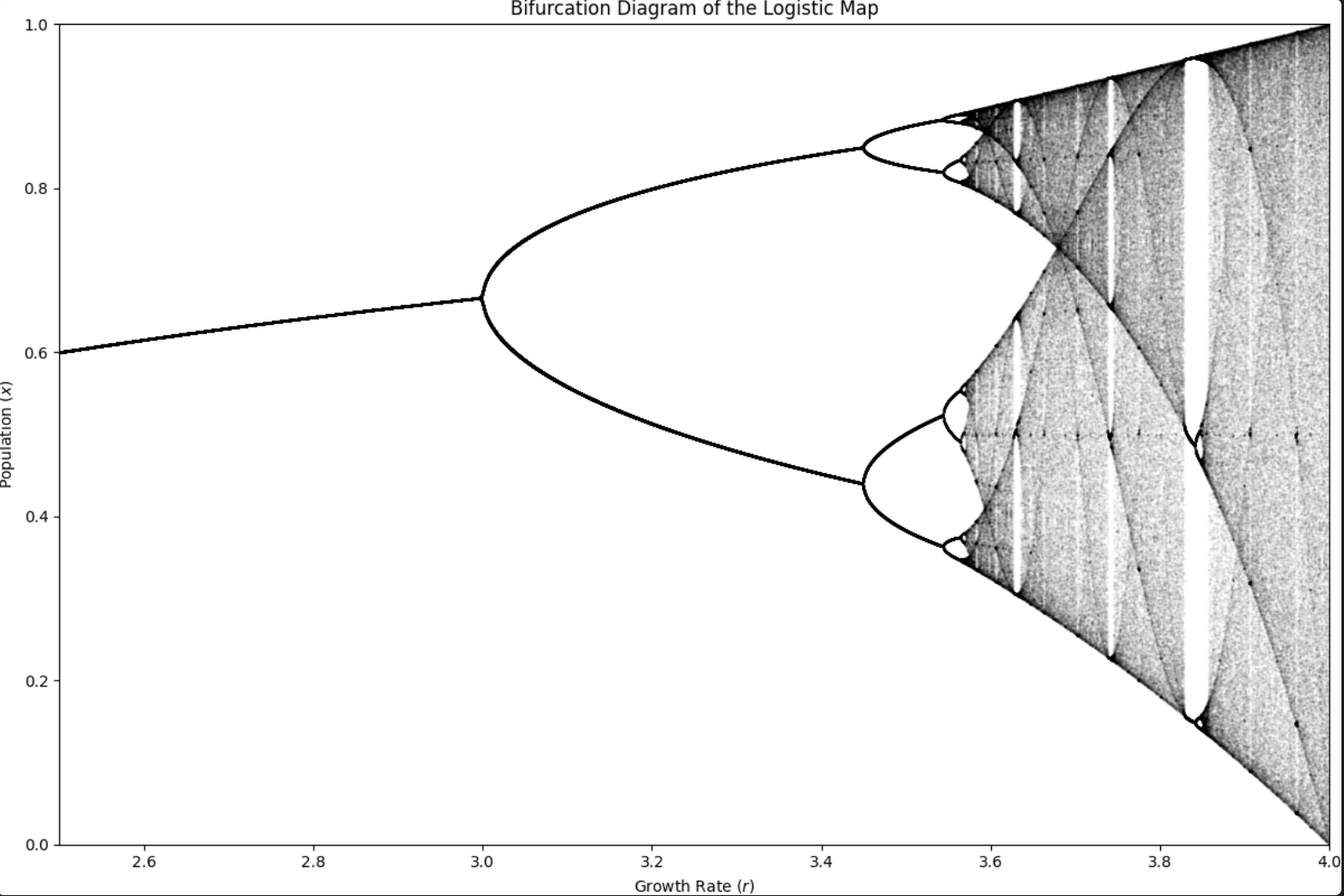
Why does this happen? It relates to the stability of fixed points and periodic orbits as we vary the parameter $r$ .

Each time a fixed point becomes unstable (derivative magnitude exceeds 1), a new periodic orbit emerges, leading to the bifurcation structure we see.

It is graphed by iterating the logistic map for many values of $r$ and plotting the long-term behavior of $x$ .

Back To Periodic Orbit Math

G (x) = 4 x (1 - x)

$G (x) = 4 x (1 - x)$ has a periodic orbit for every integer, all are sources. In fact, $G^{K}$ has $2^{K}$ fixed points.

Because each of these fixed points is a source, the periodic orbits of $G$ are all sources as well.

Graph View