Assignment 3

Problem 1

Question

(a) Prove that period-2 orbits of the Hénon Map must be of the form $\{(x,y),(y,x)\}$.

(b) Prove that the map has a period-2 orbit if and only if $4a>3(1-b{)}^2$.

Answer

A

define the henon map as:

$$H(x,y)=\{\begin{array}{l}{x}_{n+1}=1-a{x}_n^2+b{y}_n\\ y_{n+1}=x_n\end{array}$$

let $(x_0,y_0)$ be on a period 2 orbit. after one iteration:

$$(x_1,y_1)=(1-a{x}_0^2+b{y}_0,x_0)$$

thus $y_1=x_0$. applying map again must return to initial point:

$$(x_0,y_0)=(1-a{x}_1^2+b{y}_1,x_1)$$

so $y_0=x_1$.

the two orbit points are then:

$$(x_0,y_0)=(x_0,x_1)\text{and}(x_1,y_1)=(x_1,x_0)$$

Answer

setting $x=x_0$, $y=x_1$: the orbit is $\{(x,y),(y,x)\}$.

B

fixed points satisfy $H(x,y)=(x,y)$:

$$\{\begin{array}{l}x=1-a{x}^2+by\\ y=x\end{array}$$

sub second into first:

$$x=1-a{x}^2+bx$$ $$a{x}^2+x(1-b)-1=0$$

quadratic formula yields:

$$x_{\pm }=\frac{-(1-b)\pm \sqrt{(1-b{)}^2+4a}}{2a}$$

with $y_{\pm }=b{x}_{\pm }$.

period-2 orbits are fixed points of $H^2$, however not for $H$. they appear through period doubling bifrucation when a fixed point loses stability.

jacobian at fixed point $(x_{\ast },y_{\ast })$:

$$DH=\left[\begin{array}{cc}-2a{x}_{\ast }& b\\ 1& 0\end{array}\right]$$

eigenvalues from char equation:

$${\lambda }^2+2a{x}_{\ast }\lambda -b=0$$ $${\lambda }_{\pm }=-a{x}_{\ast }\pm \sqrt{a^2{x}_{\ast }^2+b}$$

bifurcation appears to happen when eigenvalue hits $-1$ so we set $\lambda =-1$:

$$1-2a{x}_{\ast }-b=0$$ $$x_{\ast }=\frac{1-b}{2a}$$

this $x_{\ast }$ must also solve the fixed point equation $a{x}^2+x(1-b)-1=0$:

$$a{\left(\frac{1-b}{2a}\right)}^2+\frac{1-b}{2a}(1-b)-1=0$$ $$\frac{(1-b{)}^2}{4a}+\frac{(1-b{)}^2}{2a}-1=0$$ $$\frac{(1-b{)}^2}{4a}+\frac{2(1-b{)}^2}{4a}=1$$ $$\frac{3(1-b{)}^2}{4a}=1$$ $$3(1-b{)}^2=4a$$

period-2 orbits exist past this bifurcation point:

Answer

$$4a>3(1-b{)}^2$$

Problem 2

Question

Find a formula for the inverse of the Hénon map with $b\ne 0$.

Answer

the henon map is:

$$H(x,y)=\{\begin{array}{l}{x}_{n+1}=1-a{x}_n^2+y_n\\ y_{n+1}=b{x}_n\end{array}$$

let $(x^{\prime },y^{\prime })=H(x,y)$, so:

$$\{\begin{array}{l}{x}^{\prime }=1-a{x}^2+y\\ y^{\prime }=bx\end{array}$$

to find $H^{-1}$, solve for $(x,y)$ in terms of $(x^{\prime },y^{\prime })$.

from the second equation:

$$y^{\prime }=bx⟹x=\frac{y^{\prime }}{b}$$

(this is why we need $b\ne 0$)

from the first equation:

$$x^{\prime }=1-a{x}^2+y⟹y=x^{\prime }-1+a{x}^2$$

sub $x=\frac{y^{\prime }}{b}$:

$$y=x^{\prime }-1+a{\left(\frac{y^{\prime }}{b}\right)}^2=x^{\prime }-1+\frac{a{y}^{\prime 2}}{b^2}$$

so the inverse is:

Answer

$$H^{-1}(x,y)=\left(\frac{y}{b},x-1+\frac{a{y}^2}{b^2}\right)$$

Problem 3

Question

For each of the following linear maps, decide whether the origin is a sink, source, or saddle fixed point. The best way to do this is to find the eigenvalues of the matrix.

(a) $A=\left[\begin{array}{cc}4& 30\\ 1& 3\end{array}\right]$

(b) $A=\left[\begin{array}{cc}\frac{1}{2}& \frac{1}{4}\\ \frac{3}{4}& \frac{1}{2}\end{array}\right]$

(c) $A=\left[\begin{array}{cc}-0.4& 2.4\\ -0.4& 1.6\end{array}\right]$

Answer

for linear map ${\vec{x}}_{n+1}=A{\vec{x}}_n$, the origin is:

• sink: all $|\lambda |<1$ (stable)
• source: all $|\lambda |>1$ (unstable)
• Saddle: mixed—some $|\lambda |<1$, some $|\lambda |>1$

eigenvalues come from $\det (A-\lambda I)=0$.

(a) $A=\left[\begin{array}{cc}4& 30\\ 1& 3\end{array}\right]$

characteristic equation:

$$\det \left[\begin{array}{cc}4-\lambda & 30\\ 1& 3-\lambda \end{array}\right]=0$$ $$(4-\lambda )(3-\lambda )-30=0$$ $$12-7\lambda +{\lambda }^2-30=0$$ $${\lambda }^2-7\lambda -18=0$$

quadratic formula:

$$\lambda =\frac{7\pm \sqrt{49+72}}{2}=\frac{7\pm \sqrt{121}}{2}=\frac{7\pm 11}{2}$$

so ${\lambda }_1=9$ and ${\lambda }_2=-2$.

Answer

Source (eigenvalues: $9,-2$)

(b) $A=\left[\begin{array}{cc}\frac{1}{2}& \frac{1}{4}\\ \frac{3}{4}& \frac{1}{2}\end{array}\right]$

characteristic equation:

$$\det \left[\begin{array}{cc}\frac{1}{2}-\lambda & \frac{1}{4}\\ \frac{3}{4}& \frac{1}{2}-\lambda \end{array}\right]=0$$ $${\left(\frac{1}{2}-\lambda \right)}^2-\frac{3}{16}=0$$ $$\frac{1}{4}-\lambda +{\lambda }^2-\frac{3}{16}=0$$ $${\lambda }^2-\lambda +\frac{1}{16}=0$$

quadratic formula:

$$\lambda =\frac{1\pm \sqrt{1-\frac{1}{4}}}{2}=\frac{1\pm \sqrt{\frac{3}{4}}}{2}=\frac{1\pm \frac{\sqrt{3}}{2}}{2}=\frac{2\pm \sqrt{3}}{4}$$

so:

$${\lambda }_1=\frac{2+\sqrt{3}}{4}\approx 0.933,{\lambda }_2=\frac{2-\sqrt{3}}{4}\approx 0.067$$

Answer

Sink (eigenvalues: $\frac{2\pm \sqrt{3}}{4}$)

(c) $A=\left[\begin{array}{cc}-0.4& 2.4\\ -0.4& 1.6\end{array}\right]$

characteristic equation:

$$\det \left[\begin{array}{cc}-0.4-\lambda & 2.4\\ -0.4& 1.6-\lambda \end{array}\right]=0$$ $$(-0.4-\lambda )(1.6-\lambda )+0.96=0$$ $$-0.64+0.4\lambda -1.6\lambda +{\lambda }^2+0.96=0$$ $${\lambda }^2-1.2\lambda +0.32=0$$

quadratic formula:

$$\lambda =\frac{1.2\pm \sqrt{1.44-1.28}}{2}=\frac{1.2\pm \sqrt{0.16}}{2}=\frac{1.2\pm 0.4}{2}$$

so ${\lambda }_1=0.8$ and ${\lambda }_2=0.4$.

Answer

Sink (eigenvalues: $0.8,0.4$)

Problem 4

Question

Let $\vec{g}(x,y)=(x^2-5x+y,x^2)$. Find and classify the fixed points of $\vec{g}$ as sinks, sources, or saddles.

Answer

Finding Fixed Points

fixed points satisfy $\vec{g}(x,y)=(x,y)$:

$$\{\begin{array}{l}x=x^2-5x+y\\ y=x^2\end{array}$$

from first equation:

$$x=x^2-5x+y⟹6x=x^2+y⟹y=6x-x^2$$

from second equation: $y=x^2$.

setting equal:

$$x^2=6x-x^2$$ $$2x^2=6x$$ $$2x(x-3)=0$$

so $x=0$ or $x=3$.

• if $x=0$: $y=0^2=0$ → fixed point $(0,0)$
• if $x=3$: $y=3^2=9$ → fixed point $(3,9)$

Classifying Fixed Points

jacobian of $\vec{g}$:

$$J=\left[\begin{array}{cc}\frac{\partial }{\partial x}(x^2-5x+y)& \frac{\partial }{\partial y}(x^2-5x+y)\\ \frac{\partial }{\partial x}(x^2)& \frac{\partial }{\partial y}(x^2)\end{array}\right]=\left[\begin{array}{cc}2x-5& 1\\ 2x& 0\end{array}\right]$$

at $(0,0)$:

$$J(0,0)=\left[\begin{array}{cc}-5& 1\\ 0& 0\end{array}\right]$$

characteristic equation:

$$\det \left[\begin{array}{cc}-5-\lambda & 1\\ 0& -\lambda \end{array}\right]=0$$ $$(-5-\lambda )(-\lambda )=0$$

so ${\lambda }_1=0$ and ${\lambda }_2=-5$.

magnitudes: $|{\lambda }_1|=0<1$ and $|{\lambda }_2|=5>1$.

mixed magnitudes → $(0,0)$ is a saddle.

at $(3,9)$:

$$J(3,9)=\left[\begin{array}{cc}2(3)-5& 1\\ 2(3)& 0\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 6& 0\end{array}\right]$$

characteristic equation:

$$\det \left[\begin{array}{cc}1-\lambda & 1\\ 6& -\lambda \end{array}\right]=0$$ $$(1-\lambda )(-\lambda )-6=0$$ $${\lambda }^2-\lambda -6=0$$

quadratic formula:

$$\lambda =\frac{1\pm \sqrt{1+24}}{2}=\frac{1\pm 5}{2}$$

so ${\lambda }_1=3$ and ${\lambda }_2=-2$.

magnitudes: $|{\lambda }_1|=3>1$ and $|{\lambda }_2|=2>1$.

both magnitudes $>1$ → $(3,9)$ is a source.

Answer

• $(0,0)$: saddle (eigenvalues $0,-5$)
• $(3,9)$: source (eigenvalues $3,-2$)

Problem 5

Question

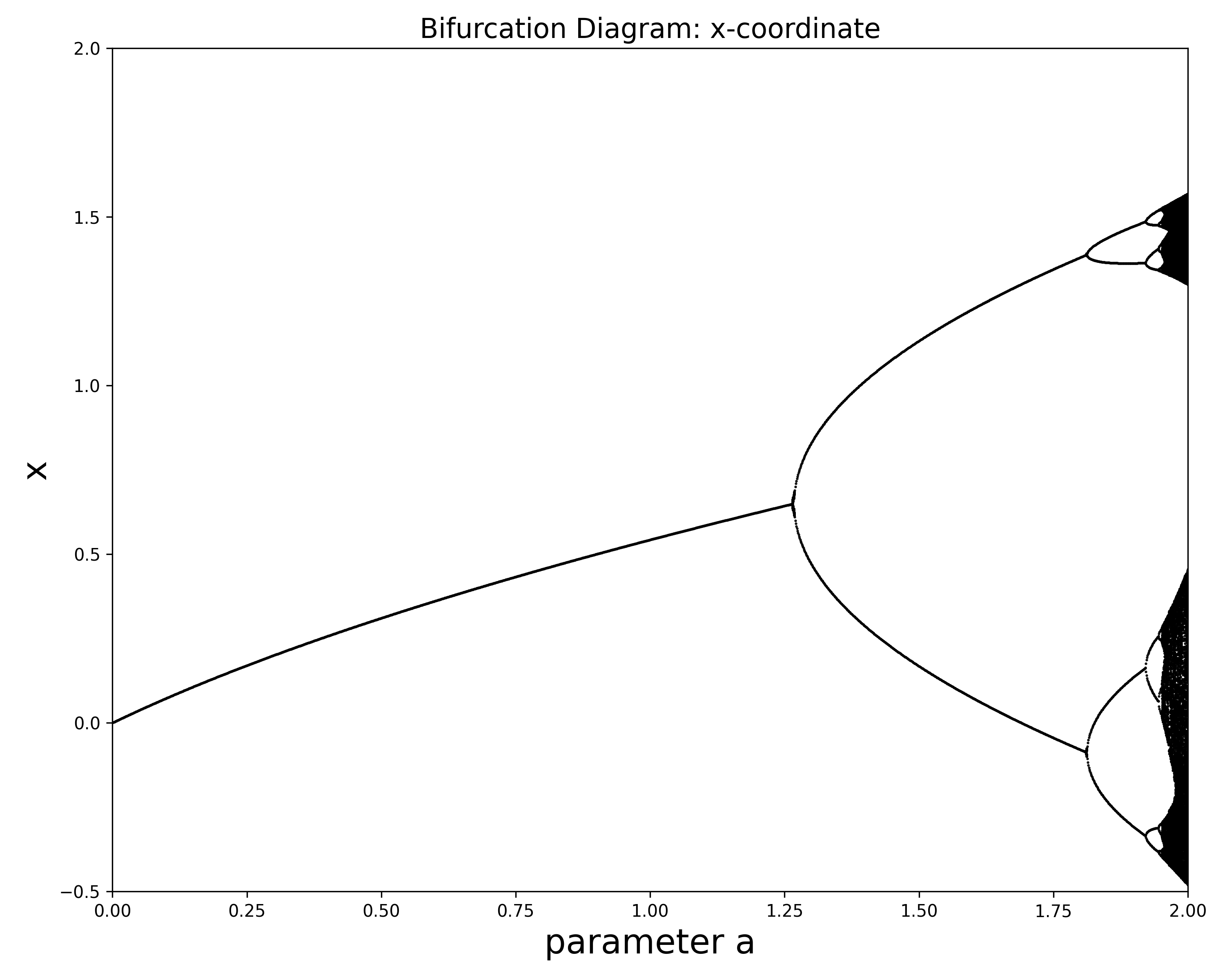
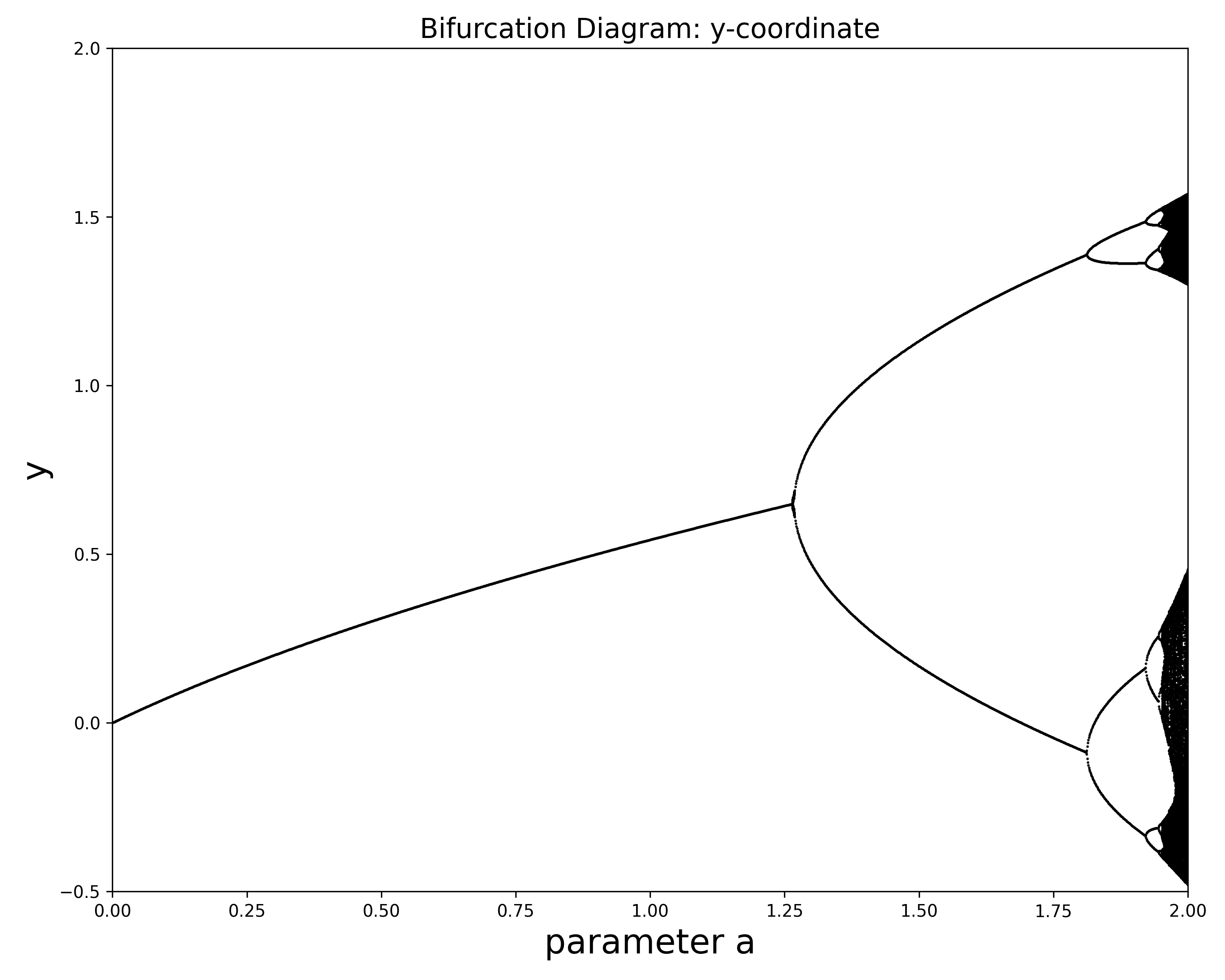
Download the file henon_bifurcation_example.m from the Code folder in the Files tab of the General channel in Teams and use it to make a bifurcation diagram like Figure 2.16. The code uses parameter $b=-0.3$ and $a$ ranging from $0$ to $2$ by increments of $da=0.001$. For each value of the parameter $a$, the code chooses the initial point $(0,2)$ and calculates its orbit under the Hénon map to step $10^4$. It then plots the last $N$ iterates ($x$-coordinates of the orbit) where $N$ is small enough to allow the orbit to settle down to the attracting set (and not crush the graphics card in your computer).

(a) Is the picture different if the $y$-coordinate is plotted instead?

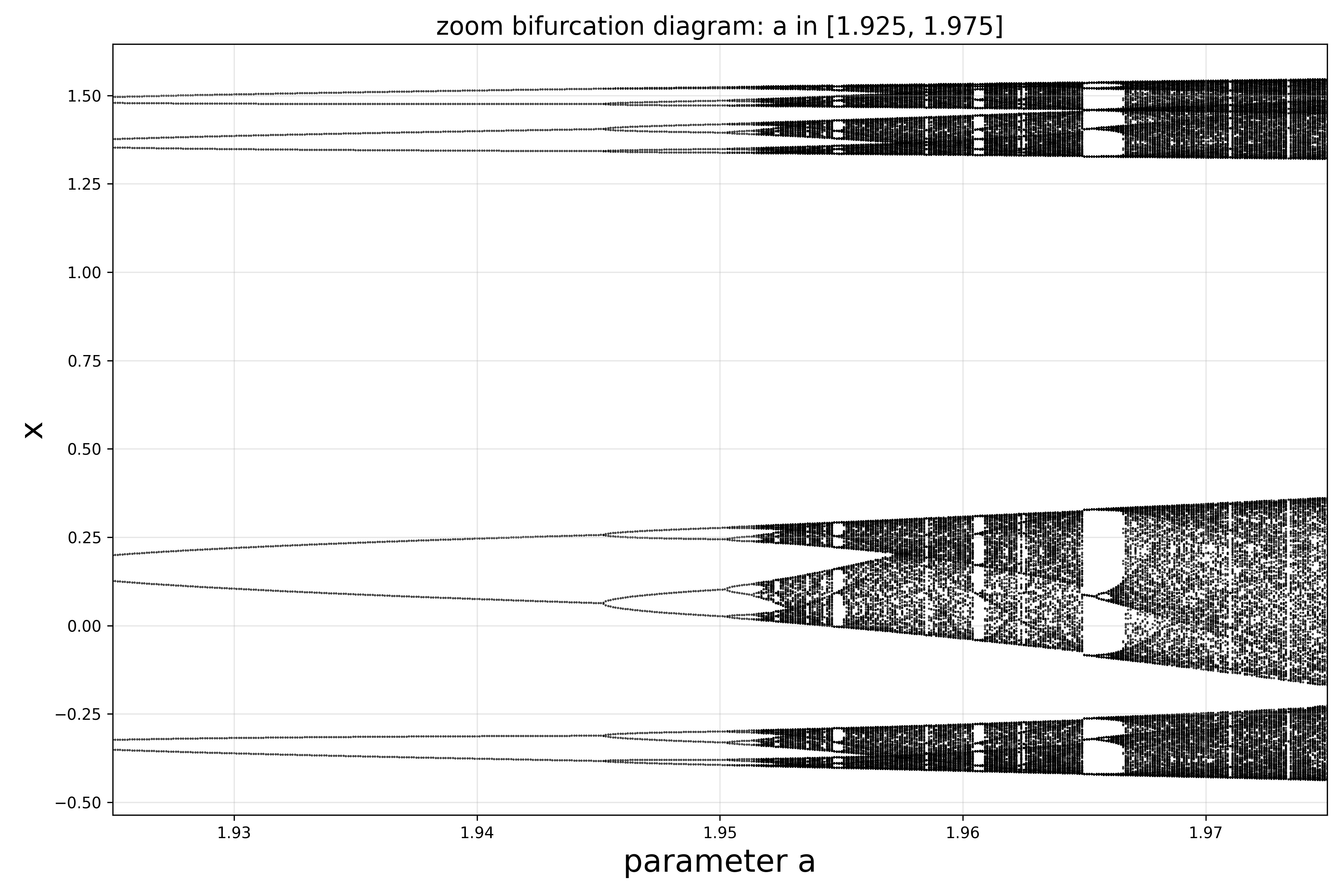
(b) Make an additional diagram varying the parameter $a$ from $1.925$ to $1.975$ by increments of $da=0.0001$. Are there any periodic windows? For which values of $a$?

(c) Generate an estimate of Feigenbaum’s constant for the period-doubling cascade using a sequence of bifurcations up to period-64. You may need to make $da$ smaller in order to resolve when a bifurcation takes place. Why doesn’t your estimate approach $\mathrm{4.669...}$?

Turn in your code, pictures, and answers to these questions.

Answer

A

the hénon map has structure:

$$\{\begin{array}{l}{x}_{n+1}=1-a{x}_n^2+b{x}_n\\ y_{n+1}=x_n\end{array}$$

given that $y_{n+1}=x_n$, $y$-coordinate is just a delayed version of $x$.

ran both versions of the code (plotting $x$ vs plotting $y$):

i found that the bifurcation diagrams were essentially identical. same structure, same bifurcation points, etc. $y$ values at any given parameter $a$ are just the $x$ values from one iteration earlier on the same attractor.

I would conclude no meaningful difference from this.

B

zoomed into $a\in [1.925,1.975]$ with $da=0.0001$ and increased iterations to $N=10^4$ for better convergence.

found that the region is mostly chaotic (dense scatter), periodic windows rare + narrow. Found some periodic behavior at:

• $a\approx 1.925$: period-8 window
• $a\approx 1.973$: period-32 window

islands of order in a sea of insanity. appear as verticle lines of discrete points in the burfrucation diagram rather than filled chaotic regions.

C

scanned parameter space from $a=1.0$ to $1.5$ looking for period-doubling bifurcations up to period-64.

why not approaching 4.669…?

feigenbaum’s constant $\delta \approx 4.669\dots$ IS universal for the hénon map in that it applies to any smooth dissapating map with quadratic extrema, however thisi s a 1d map. henon maps period doubling cascade converges to the same $\delta$ in limit.

the numerical estimate fails for practical reasons, namely that the resolution and accuracy required to see convergence is very high. each successive bifurcation gets closer together, and with finite step size and numerical precision, we can’t resolve them well enough. we also have the problem of detection sensitivity when locating bifurcations on a discrete grid.

to get a better estimate: use adaptive refinement or root-finding to locate each bifurcation precisely, then compute successive ratios.

Code

Python

import numpy as np import matplotlib.pyplot as plt def henon_bifurcation(coord="x", amin=0.0, amax=2.0, b=-0.3, N=10**3, da=10**-3): x = np.zeros(N + 1) y = np.zeros(N + 1) a_vals, coord_vals = [], [] for a in np.arange(amin, amax + da/2, da): x[0], y[0] = 0.0, 2.0 for i in range(N): x[i+1] = a - x[i]**2 + b*y[i] y[i+1] = x[i] # detect period data = x if coord == "x" else y p = 9 for j in range(10): if np.abs(data[-1] - data[-1 - 2**j]) < 1e-5: p = j break pts = data[-2**p:] coord_vals.extend(pts) a_vals.extend([a] * len(pts)) return a_vals, coord_vals def detect_period(a, b=-0.3, N=15000): x = np.zeros(N + 1) y = np.zeros(N + 1) x[0], y[0] = 0.0, 2.0 for i in range(N): x[i+1] = a - x[i]**2 + b*y[i] y[i+1] = x[i] for power in range(8): p = 2**power if p > N // 4: break matches = sum(abs(x[-1-i] - x[-1-i-p]) < 1e-5 for i in range(min(p*2, 100))) if matches / min(p*2, 100) > 0.9: return p return -1 # part (a): x vs y coordinates a_x, x_vals = henon_bifurcation(coord="x") plt.figure(figsize=(10, 8)) plt.scatter(a_x, x_vals, c="k", s=1, marker=".") plt.xlabel("parameter a", fontsize=20) plt.ylabel("x", fontsize=20) plt.title("Bifurcation Diagram: x-coordinate", fontsize=16) plt.ylim([-0.5, 2]) plt.xlim([0, 2]) plt.tight_layout() plt.savefig("part_a_x_coordinate.png", dpi=300) plt.close() a_y, y_vals = henon_bifurcation(coord="y") plt.figure(figsize=(10, 8)) plt.scatter(a_y, y_vals, c="k", s=1, marker=".") plt.xlabel("parameter a", fontsize=20) plt.ylabel("y", fontsize=20) plt.title("Bifurcation Diagram: y-coordinate", fontsize=16) plt.ylim([-0.5, 2]) plt.xlim([0, 2]) plt.tight_layout() plt.savefig("part_a_y_coordinate.png", dpi=300) plt.close() # part (b): zoom a_zoom, x_zoom = henon_bifurcation(coord="x", amin=1.925, amax=1.975, N=10**4, da=10**-4) plt.figure(figsize=(12, 8)) plt.scatter(a_zoom, x_zoom, c="k", s=0.5, marker=".") plt.xlabel("parameter a", fontsize=20) plt.ylabel("x", fontsize=20) plt.title("zoom bifurcation diagram: a in [1.925, 1.975]", fontsize=16) plt.xlim([1.925, 1.975]) plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig("part_b_zoom.png", dpi=300) plt.close() # part (c): feigenbaum constant periods = [(a, detect_period(a)) for a in np.linspace(1.0, 1.5, 2000)] bifurcations = [] for i in range(1, len(periods)): if periods[i-1][1] > 0 and periods[i][1] > 0: if periods[i][1] == 2 * periods[i-1][1]: bifurcations.append((periods[i-1][1], periods[i][0])) if bifurcations: print(f"found {len(bifurcations)} bifurcations:") for p, a in bifurcations: print(f" period {p} -> {2*p} at a \approx {a:.6f}") if len(bifurcations) >= 3: print("\nfeigenbaum estimates:") for i in range(len(bifurcations) - 2): a1, a2, a3 = bifurcations[i][1], bifurcations[i+1][1], bifurcations[i+2][1] if abs(a3 - a2) > 1e-8: print(f" δ_{i+1} ≈ {(a2 - a1) / (a3 - a2):.6f}")

Output

Figures