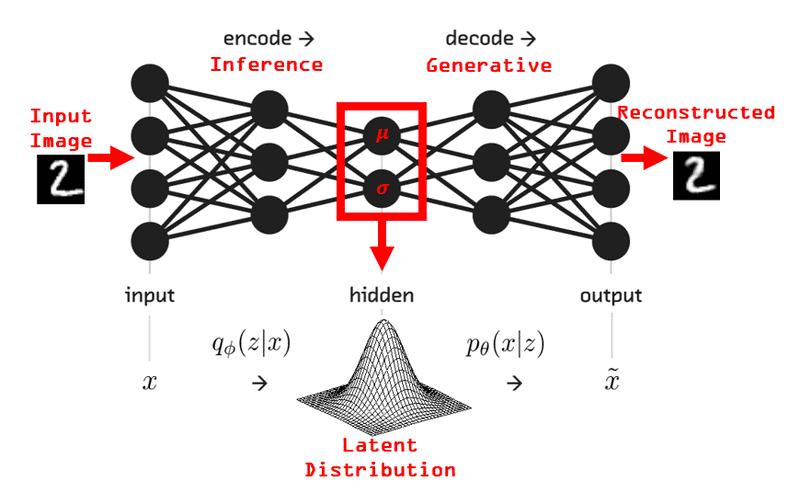
Variational Autoencoder

Variational Autoencoders (VAE) fundamentally transform the goal of neural networks from learning a direct mapping from inputs to outputs, to learning a probabilistic representation of the data. This is achieved by encoding the input data into a latent space defined by a probability distribution, typically a Gaussian distribution characterized by its mean and variance.

This is especially useful for generative tasks like diffusion models, where the goal is to generate new data samples that resemble the training data, but are not identical to any specific training example. By sampling from the learned latent space, VAEs can produce diverse outputs that capture the underlying structure of the data. Now, instaed of generating a single output for a given input, the model takes a sample from its learned probabilisty distribution, allowing for variability and creativity in the generated outputs.

---

Formal Formulation

There are a few ways to implement a VAE, but the most common approach is to use a neural network to parameterize the mean and variance of the latent space distribution. Given that this is a Gaussian, that means only two parameters are needed. The encoder network takes the input data and outputs the mean ($\mu$) and log-variance ($\log ({\sigma }^2)$) of the latent space distribution. The log-variance is used instead of variance directly to ensure numerical stability and to keep the variance positive.

We want to maximize the likelihood of the data given the latent variables, which for a probability distribution $p_{\theta }(x)=p(x|\theta )$ can be expressed as the following marginalizing over $z$:

$$p_{\theta }(x)={\int }_z{p}_{\theta }(x,z)dz$$

Where $p_{\theta }(x,z)$ is the joint distribution under the model, which can be decomposed using the chain rule of probability:

Doing this, we can rewrite the marginal likelihood as:

$$p_{\theta }(x)={\int }_z{p}_{\theta }(x|z)p_{\theta }(z)dz$$

Where:

• $p_{\theta }(z)$ - the prior distribution over the latent variables, typically a standard normal distribution $N(0,I)$.
• $p_{\theta }(x|z)$ - the likelihood of the data given the latent
• $p_{\theta }(z|x)$ - the posterior distribution of the latent variables given the data, which is intractable to compute directly.

---

Training Objective: The ELBO

It is intractable to train a VAE directly by maximizing the marginal likelihood $p_{\theta }(x)$, because it involves integrating over all possible values of the latent variables $z$. Instead, we optimize a lower bound on the log marginal likelihood called the Evidence Lower Bound (ELBO).

The ELBO can be written as:

$$\mathcal{L}(\theta ,\varphi ;x)={\mathbb{E}}_{q_{\varphi }(z|x)}\left[\log p_{\theta }(x|z)\right]-D_{KL}(q_{\varphi }(z|x)\Vert p_{\theta }(z))$$

This decomposes into two intuitive terms:

• Reconstruction term: How well we can reconstruct $x$ from the latent code $z$
• Regularization term: How close our learned posterior $q_{\varphi }(z|x)$ is to the prior $p_{\theta }(z)$

The ELBO satisfies $\log p_{\theta }(x)\ge \mathcal{L}(\theta ,\varphi ;x)$, with the gap being exactly the KL divergence between the approximate and true posteriors. By maximizing the ELBO, we simultaneously:

1. Improve the generative model (increase log evidence)
2. Make the approximate posterior closer to the true posterior

For a detailed derivation, intuition, and the reparameterization trick, see Evidence Lower Bound.