Double Descent is a fairly recent discovery in the field of machine learning and statistics that challenges traditional notions of model complexity and generalization error. It describes a phenomenon where increasing the complexity of a model beyond a certain point can lead to a decrease in generalization error, resulting in a “double descent” curve when plotting error against model complexity.
This is particularly interesting, as the models are oftentimes still doing what we consider “overfitting” in traditional statistics(by memorising the noise in the training data), yet they still manage to generalize well to unseen data.
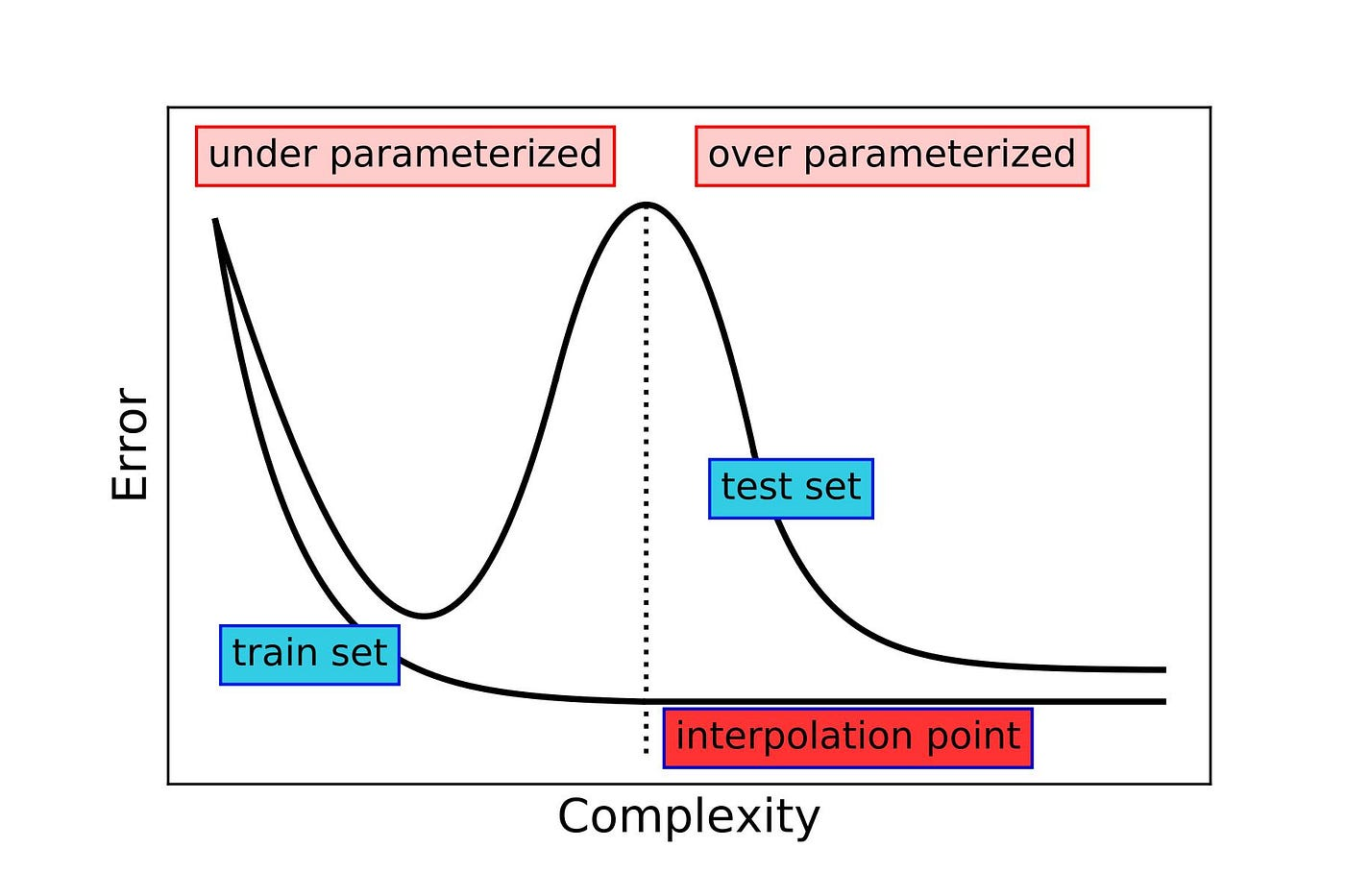
Why does Double Descent occur?
While the exact mechanisms behind Double Descent are still being studied, several hypotheses have been proposed:
- The Role of Interpolation: In the over-parameterized regime, models can perfectly interpolate the training data. However, this interpolation can lead to a form of implicit regularization that helps the model generalize better.
- Model Averaging: Over-parameterized models can be seen as ensembles of simpler models, which can lead to better generalization through a form of model averaging.
- Implicit Bias of Optimization Algorithms: The optimization algorithms used to train these models (like stochastic gradient descent) may have an implicit bias towards solutions that generalize well, even in the presence of overfitting.