Homework 9 Written

---

Sequence Alignment: Algorithm Tracing

Consider two sequences of characters “opt” and “cope” and the misalignment penalty specification shown below.

Penalties:

• Gap penalty $\delta =2$
• Mismatch penalty $a_{ij}=0$ if aligning the same vowels or consonants
• Mismatch penalty $a_{ij}=1$ if aligning different vowels or consonants
• Mismatch penalty $a_{ij}=3$ if aligning a vowel and a consonant

The pseudocode of the sequence alignment algorithm is shown below. (For the two sequences above, m = 3 for “opt” and n = 4 for “cope”.)

Trace the sequence alignment algorithm as we did in class. Specifically,

1. Create an fill in a two-dimensional memorization array $M[\mathrm{0..3},\mathrm{0..4}]$ shown below (3 and 4 are the numbers of characters in “opt” and “cope”, respectively).

In your answer, each array cell should contain the minimum alignment cost and the immediate predecessor array cell. Show the immediate predecessor array cell using an arrow as shown in the example below (left). If there is a tie among the three cases, show both arrows.

2. Show the optimal alignment (i.e., with the minimum misalignment penalty) with red color arrows in the memoization table (see the example below (left)) and also in a box-sequence diagram (see the example below (right)). If there are more than one optimal alignment (i.e., with the same minimum alignment cost), write all of them in the answer.

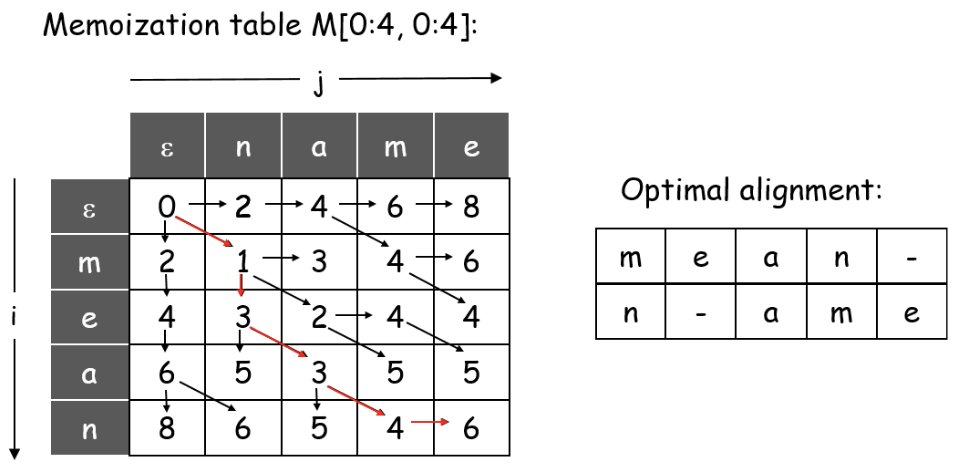
Building Memoization Table

We know $x=\text{opt}$ and $y=\text{cope}$, gap penalty $\delta =2$, and mismatch penalties $\alpha [x_i,y_j]$ yields 0 for same vowels/consonants, 1 for different vowels/consonants, and 3 for vowel vs consonant.

We initialize $M[i,0]=i\times \delta$ for first col, and $M[0,j]=j\times \delta$ for the first row. Then we fill rest with:

$$M[i,j]=min(\alpha [x_i,y_j]+M[i-1,j-1],\delta +M[i-1,j]\delta +M[i,j-1])$$

Yielding: see figure 4

Optimal Alignments

Minimum cost = 5, therefore tracing from $M[3,4]$ with red path yields:

$$M[0,0]\to M[0,1]\to M[1,2]\to M[2,3]\to M[3,4]$$

Yielding Optimal algorithm: see figure 5

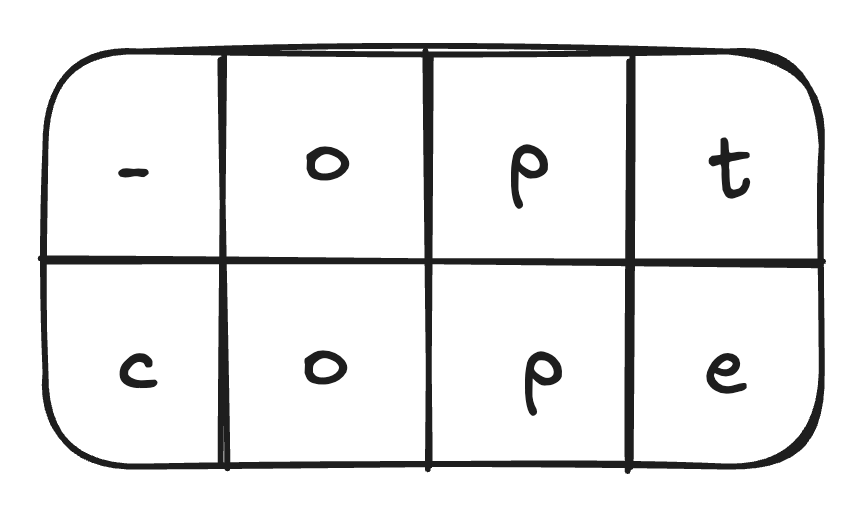
Cost: gap + $c$ + $o$ + $o$ + $p$ + $p$ + $t$ + $e$ = 5, meaning optimal alignment.

---

Bellman-Ford Shortest Paths: Algorithm Tracing

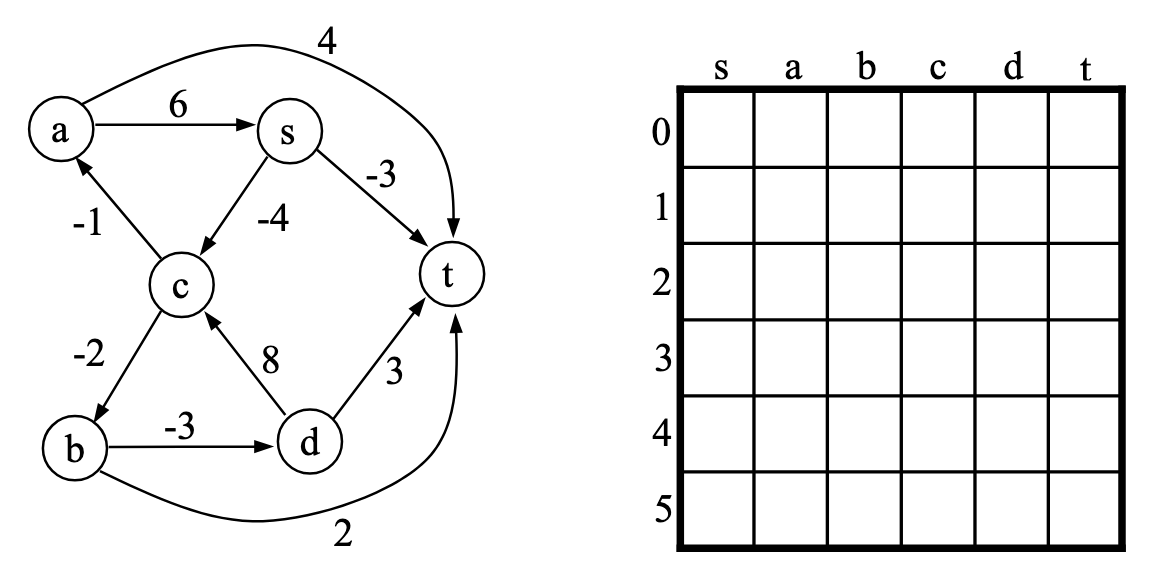
Consider the directed graph shown below (left). Run the Bellman-Ford shortest path algorithm we studied in class to find the shortest path from each node to the node t. Specifically,

1. Fill in the two-dimensional memorization array $M[\mathrm{0..}n,V]$ shown below (right) (n: the number of nodes, V: the set of nodes), where each array entry contains the shortest path length and the immediate successor node. Show the completed memorization table with “shortest path length/immediate successor” in each array entry, e.g., “8/d”
2. For each node in the graph, show the shortest path and its path length in the following format: “Shortest path from x to t: x – y – z – t (path length = 8)”. Note path length is the sum of the weights of edges in the path. Showing the intermediate steps of computing the shortest path length is not required but is recommended for partial credit in case of an incorrect answer.

Memoization Table

We know this table shows us the shortest path from node $v$ to $t$ with at most $i$ edges, along immediately after the successor node.

We can use Bellman Ford Recurrence here:

$$M[i,v]=min(M[i-1,v],\text{min over all edges }(v\to u)of\{weight(v,u)+M[i-1,u]\})$$

Yielding:

See figure 7

Shortest Paths

Using the previous final row at $i=5$ we can trace:

$$\begin{array}{rl}\text{1. Shortest path from }s\text{ to }t:& s\to c\to b\to d\to t\text{(path length }=-6\text{)}\\ & \text{Verification: }-4+(-2)+(-3)+3=-6\\ \text{2. Shortest path from }a\text{ to }t:& a\to s\to c\to b\to d\to t\text{(path length }=0\text{)}\\ & \text{Verification: }6+(-4)+(-2)+(-3)+3=0\\ \text{3. Shortest path from }b\text{ to }t:& b\to d\to t\text{(path length }=0\text{)}\\ & \text{Verification: }-3+3=0\\ \text{4. Shortest path from }c\text{ to }t:& c\to b\to d\to t\text{(path length }=-2\text{)}\\ & \text{Verification: }-2+(-3)+3=-2\\ \text{5. Shortest path from }d\text{ to }t:& d\to t\text{(path length }=3\text{)}\\ & \text{Verification: }3=3\\ \text{6. Shortest path from }t\text{ to }t:& t\text{(path length }=0\text{)}\\ & \text{No movement required}\end{array}$$