Homework 7 Written

---

Integer Multiplication: Reading & Research

(This exercise is for your own reading and research based on a textbook chapter we skipped in class.) Read the discussion on Integer Multiplication algorithm using divide-and-conquer in Section 5.5 of the textbook (pages 231 – 234 provided below), and provide answers as specified below. Assume the integers multipled are binary integers.

1. Write the key idea that enables the algorithm to divide the problem into three disjoint subproblems — that is, to achieve the multiplication of two n-bit integers from multiplying two n/2-bit integers three times.

2. Write the resulting divide-and-conquer algorithm in an executable pseudocode. Name the algorithm “MultInt”. Do not copy the pseudocode in the texbook but write your own pseudocode. Make sure to add the base case; the textbook code may not have the base case. Make use of the following functions as needed in your pseudocode.

• MultInt(x, y, n) returns the multiplication of two n-bit integers x and y.
• Add(x, y, n) returns the sum of two n-bit integers x and y, i.e., x + y.
• Sub(x, y, n) returns the difference of n-bit integer y from n-bit integer x, i.e., x – y. LSL(x, b) returns x shifted to the left logically by b bits. (Logical shift left (LSL) shifts in bit 0’s on the least significant bits.)
• LSR(x, b) returns x shifted to the right logically by b bits. (Logical shift right (LSR) shifts in bit 0’s on the most significant bits.)
• ceil(b) returns the ceiling of b.
• floor(b) returns the floor (i.e., truncation)of b.

Note:

• Dividing (i.e., separating) an n-bit integer into the upper n/2-bit integer and the lower n/2-bit integer can be implemented in linear time by calling logical-shift by n/2 bits (LSL and LSR below).

• Multiplying an integer by 2n can be implemented in linear time by calling logical- shift left by n bits.

1. Write a recurrence relation that expresses the run-time, T(n), of the recursive algorithm, and explain how each term in the recurrence relation is formed.

2. Write the steps of solving the recurrence relation to derive the run-time complexity T(n) = O(nlg3) (=O(n1.585)). (Here, lg3 $\equiv$ log23.) Use the recursion tree technique to derive the run- time complexity; make a simplifying assumption that n is a power of 2 integer. Do not use the master theorem in Section 5.2. There is no need to give a formal proof of big-O.

1. Key Idea

Our key idea that allows us to divide our problem into 3 smaller problems is to use the following formula instead of just the 4 products by factoring:

$$(x_1+x_0)(y_1+y_0)=x_1{y}_1+x_1{y}_0+x_0{y}_1+x_0{y}_0$$

Henceforth, we can do $x_1{y}_1$ recursively, $x_0{y}_0$ recursively, and $(x_1+x_0)(y_1+y_0)$ recursively, we can get the desired middle term using subtraction:

$$(y_1+y_0)-x_1{y}_1-x_0{y}_0=x_1{y}_0+x_0{y}_1$$

Leaving us with a problem of only 3 recursive multiplacions, which greatly reduces time complexity.

2. Pseudocode

See figure 1(may be on a different page due to latex compilation quirks.

3. Recurrence Relation

For a running time $T(n)$:

$$T(n)\le 3T\left(\frac{n}{2}\right)+cn$$

where we imagine $c$ to represent a constant.

The $3T\left(\frac{n}{2}\right)$ is the 3 recursive call structure we had before, $cn$ is the divide/conquer overhead(given than both divide and conquer operations are $O(n)$).

4. Recurrence Solutino with Recurrence Tree

$$T(n)=3T\left(\frac{n}{2}\right)+cn$$

where we assume that $n=2^k$ for an integer $k$, and where $n$ is a power of $2$.

Performing recursion tree analysis yields:

$$\begin{array}{rl}\text{Level 0: }& 1\text{ node with cost }cn\Rightarrow cn\\ \text{Level 1: }& 3\text{ nodes, cost }c(n/2)\text{ each}\Rightarrow 3\cdot c(n/2)=\frac{3}{2}cn\\ \text{Level 2: }& 3^2=9\text{ nodes, cost }c(n/4)\text{ each}\Rightarrow 9\cdot c(n/4)={\left(\frac{3}{2}\right)}^{2}cn\\ \text{Level }i:& 3^i\text{ nodes, cost }c(n/2^i)\text{ each}\Rightarrow 3^i\cdot c(n/2^i)={\left(\frac{3}{2}\right)}^{i}cn\end{array}$$

And the tree height:

$$\begin{array}{rl}T(n)& =\sum _{i=0}^{{\log }_{2}n}{\left(\frac{3}{2}\right)}^{i}cn\text{(geometric series with }r=3/2>1\text{)}\\ & =cn\cdot \frac{{\left(\frac{3}{2}\right)}^{{\log }_{2}n+1}-1}{\frac{3}{2}-1}\text{(using }\sum _{i=0}^k{r}^i=\frac{r^{k+1}-1}{r-1}\text{)}\\ & =cn\cdot \frac{{\left(\frac{3}{2}\right)}^{{\log }_{2}n+1}-1}{\frac{1}{2}}\\ & =2cn\cdot \left[{\left(\frac{3}{2}\right)}^{{\log }_{2}n+1}-1\right]\\ & \approx 2cn\cdot {\left(\frac{3}{2}\right)}^{{\log }_{2}n+1}\text{(dominant term)}\\ & =2cn\cdot \frac{3}{2}\cdot {\left(\frac{3}{2}\right)}^{{\log }_{2}n}\\ & =3cn\cdot {\left(\frac{3}{2}\right)}^{{\log }_{2}n}\\ & =3cn\cdot \frac{3^{{\log }_{2}n}}{n}\\ & =3c\cdot 3^{{\log }_{2}n}\\ & =3c\cdot n^{{\log }_{2}3}\text{(since }{3}^{{\log }_{2}n}=n^{{\log }_{2}3}\text{)}\\ & =O(n^{{\log }_{2}3})=O(n^{1.585})\end{array}$$

---

Weighted Interval Scheduling: Algorithm Tracing

Consider the dynamic programming algorithm we discussed for the weighted interval scheduling problem. Run the bottom-up (i.e., iterative) implementation of the algorithm on the problem instance shown below. Show the algorithm trace in the same manner as in Figure 6.5(a) and (b) (page 260) of the textbook - specifically, show in your answer:

1. The plot of sorted jobs
2. The list of values of $p(i)$ for each job $i(i=\mathrm{1..8})$. (Note thte job numbers here are the number after the sorting.)
3. The memoization table (array) filled in after each iteration of the algorithm, with arrows pointing to the array entries containing solutions to the two subproblems.
4. the set of jobs selected as sa result. (There are two alternative optimal sets of jobs possible with the algoirthm; either one can be given as the answer)

1. Sort Job by Finishing time

$$\begin{array}{rl}\text{Job 1:}& [2,4],\text{ value}=3\\ \text{Job 2:}& [2,4],\text{ value}=5\\ \text{Job 3:}& [4,6],\text{ value}=5\\ \text{Job 4:}& [4,7],\text{ value}=8\\ \text{Job 5:}& [5,7],\text{ value}=3\\ \text{Job 6:}& [6,9],\text{ value}=7\\ \text{Job 7:}& [7,10],\text{ value}=3\\ \text{Job 8:}& [9,11],\text{ value}=4\end{array}$$

Jobs sorted by finish time as a gantt diagram made using mermaid: see figure 03

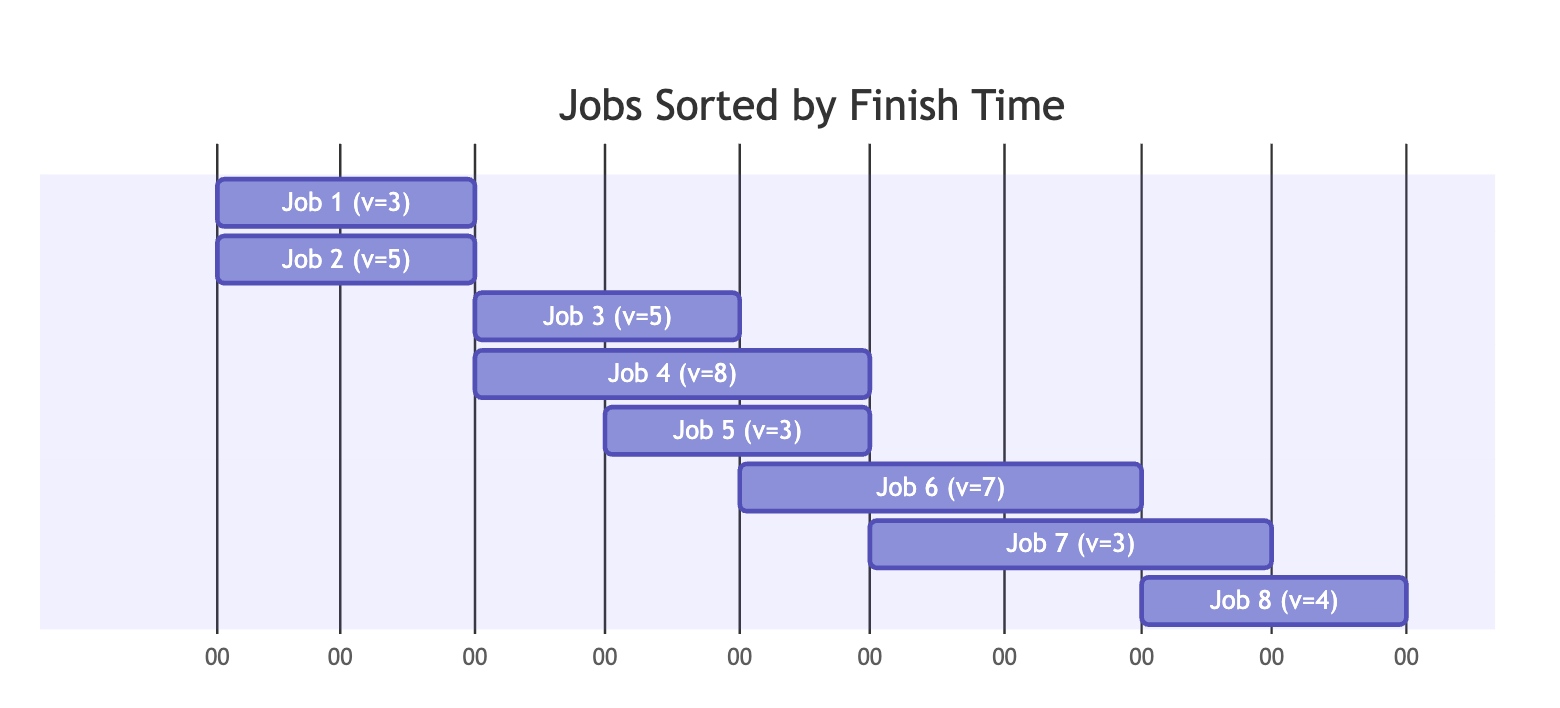
2. COmpute $p(i)$ Values

Given each job $i$, we know that $p(i)$ is the largest index $j<i$ where job $j$ is compatible with job $i$.

$$\begin{array}{rl}p(1)& =0\\ p(2)& =0\\ p(3)& =2\\ p(4)& =2\\ p(5)& =2\\ p(6)& =3\\ p(7)& =5\\ p(8)& =6\end{array}$$

3. Memoization Table

Where we set recurrence $M[i]$ as $max(v_i+M[p(i)],M[i-1])$:

$$\begin{array}{rl}M[0]& =0\\ M[1]& =\max (3+M[0],M[0])=\max (3,0)=3\\ M[2]& =\max (5+M[0],M[1])=\max (5,3)=5\\ M[3]& =\max (5+M[2],M[2])=\max (10,5)=10\\ M[4]& =\max (8+M[2],M[3])=\max (13,10)=13\\ M[5]& =\max (3+M[2],M[4])=\max (8,13)=13\\ M[6]& =\max (7+M[3],M[5])=\max (17,13)=17\\ M[7]& =\max (3+M[5],M[6])=\max (16,17)=17\\ M[8]& =\max (4+M[6],M[7])=\max (21,17)=21\end{array}$$

Yielding a final array of:

$$[0,3,5,10,13,13,17,17,21]$$

4. Optimal Solution

We can find this by performing a traceback to find our selected jobs:

$$\begin{array}{rl}M[8]& =21=4+M[6]\to Includejob8,goM[6]\\ M[6]& =17=7+M[3]\to Includejob6,goM[3]\\ M[3]& =10=5+M[2]\to Includejob3,goM[2]\\ M[2]& =5=5+M[0]\to Includejob2,STOP\end{array}$$

Then, using selected jobs $\{2,3,6,8\}$:

$$\begin{array}{rl}Jo{b}_2& :[2,4],value=5\\ Jo{b}_3& :[4,6],value=5\\ Jo{b}_6& :[6,9],value=7\\ Jo{b}_8& :[9,11],value=4\end{array}$$

Yielding a total value of $21$.