Homework 6 Written

---

Counting Inversion: Algorithm Tracing

Consider the counting inversion algorithm. Sort-and-Count studied in class and shown below.

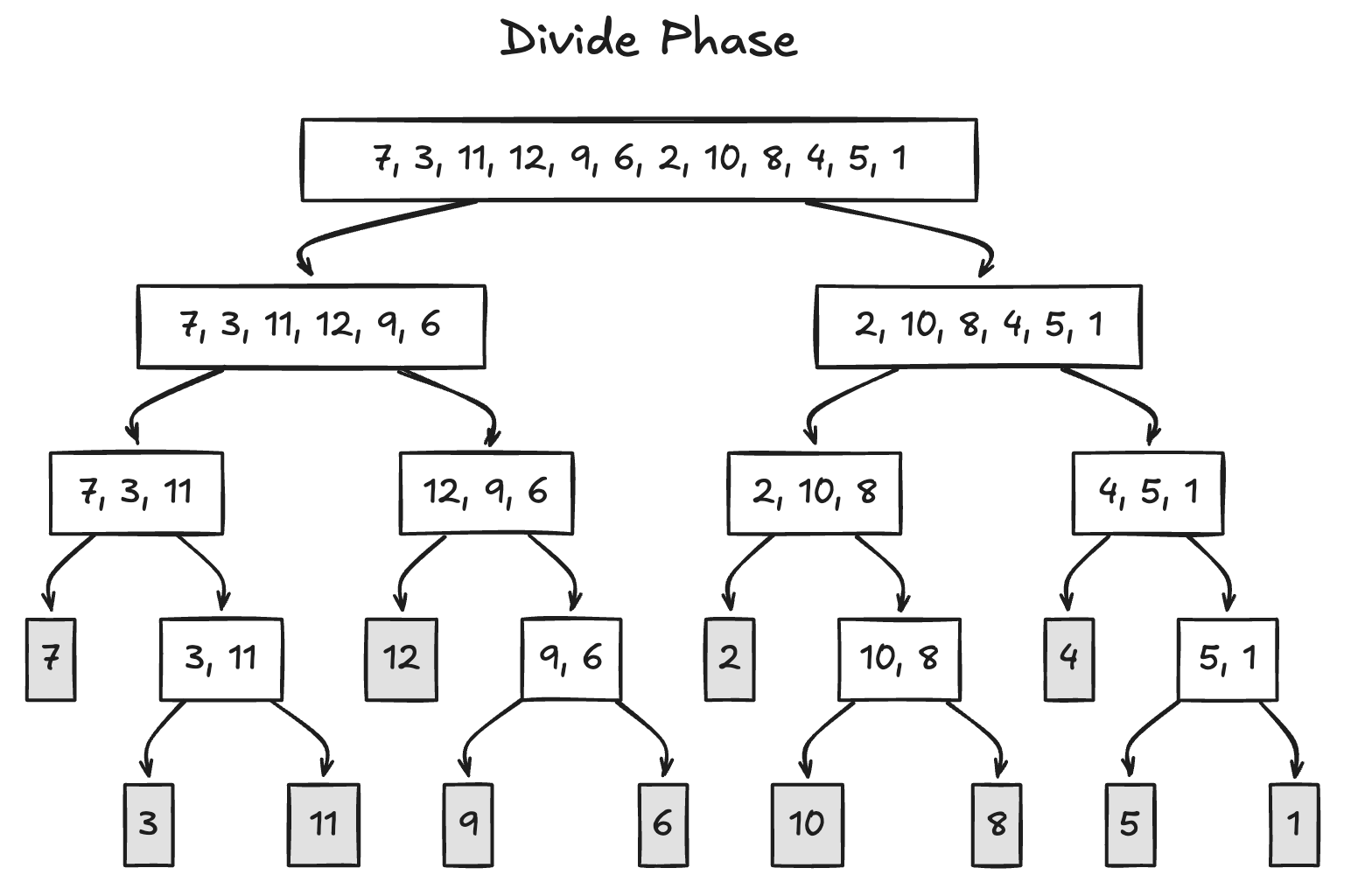
Run this algorithm against the input file shown below, and:

1. Show the recursion tree during the divide phase and the conquer & combine phase, respectively, and
2. Show each returned result as the pair of the inversion count and the sorted result (e.g., “(1, {4, 6})”) exactly in the order of execution. If the input array has an odd number of elements, the left half contains one fewer element than the right half. See the example recursion trees below.

Input file:

$$\{7,3,11,12,9,6,2,10,8,4,5,1\}$$

Example Recursion tree for an input file:

$$\{6,4,2,3\}$$

1. Divide and Conquer Phase Diagrams

See Figure 2 and Figure 3(may be on a separate page due to LaTeX compilation bs

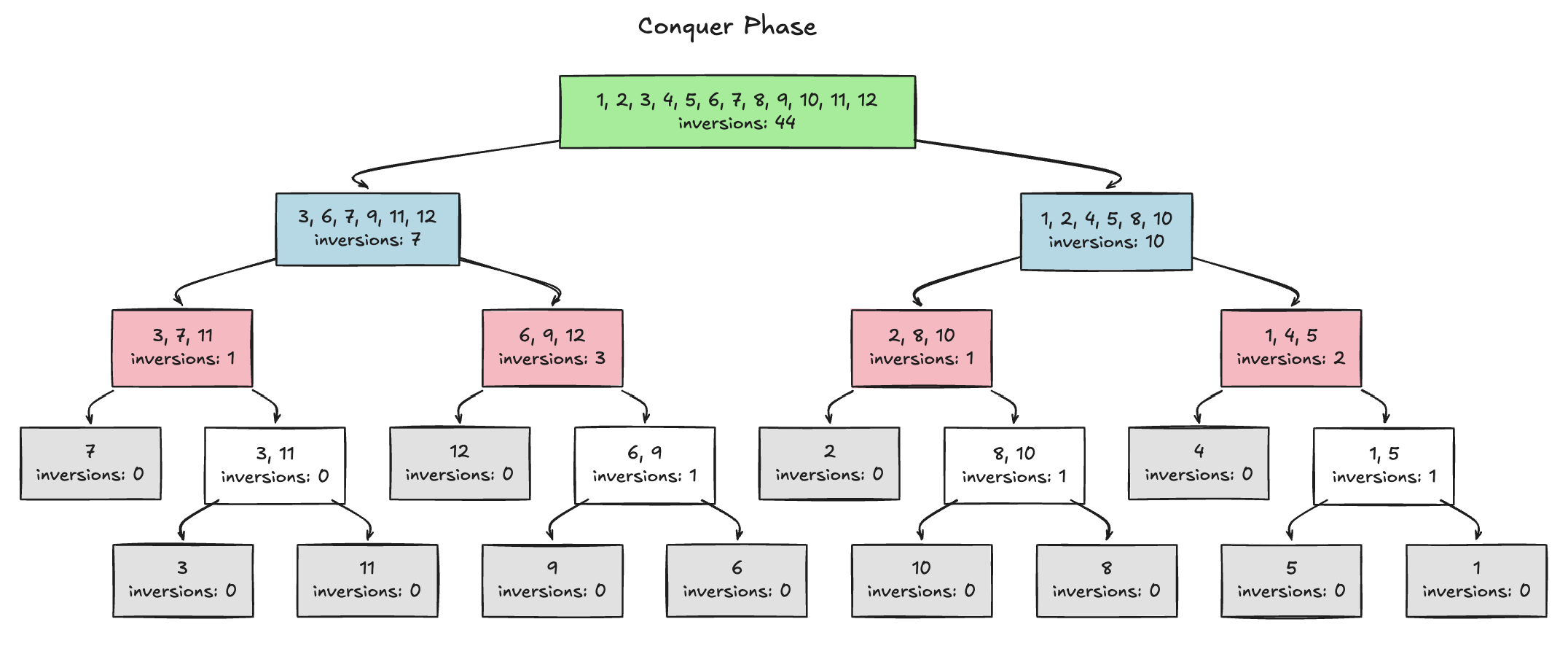
2. Returned Results in Execution Order

$$\begin{array}{rl}\text{Step 1:}& (0,\{7\})\\ \text{Step 2:}& (0,\{3\})\\ \text{Step 3:}& (0,\{11\})\\ \text{Step 4:}& (0,\{3,11\})\\ \text{Step 5:}& (1,\{3,7,11\})\\ \text{Step 6:}& (0,\{12\})\\ \text{Step 7:}& (0,\{9\})\\ \text{Step 8:}& (0,\{6\})\\ \text{Step 9:}& (1,\{6,9\})\\ \text{Step 10:}& (3,\{6,9,12\})\\ \text{Step 11:}& (7,\{3,6,7,9,11,12\})\\ \text{Step 12:}& (0,\{2\})\\ \text{Step 13:}& (0,\{10\})\\ \text{Step 14:}& (0,\{8\})\\ \text{Step 15:}& (1,\{8,10\})\\ \text{Step 16:}& (1,\{2,8,10\})\\ \text{Step 17:}& (0,\{4\})\\ \text{Step 18:}& (0,\{5\})\\ \text{Step 19:}& (0,\{1\})\\ \text{Step 20:}& (1,\{1,5\})\\ \text{Step 21:}& (2,\{1,4,5\})\\ \text{Step 22:}& (10,\{1,2,4,5,8,10\})\\ \text{Step 23:}& (44,\{1,2,3,4,5,6,7,8,9,10,11,12\})\end{array}$$

---

Divide and Conquer: Majority Equivalence Class

Do Textbook Exercise 3 in Chapter 5. Note that the problem of finding a set of more than half the bank cards that correspond to the same account can be reduced to finding a majority equivalence class, that is, an equivalence class that contains more than half the set elements (i.e., bank cards). Assume that the equivalence tester requires two cards to give a test result. Give your answers as specified below.

1. [Property] Prove the property that if there exists a majority equivalence class in the set of size n then at least one of the two halves (each of size n/2) has a majority equivalence class. Suggested proof technique: proof by contradiction.
2. [Algorithm] Based on the proven property, write an executable pseudocode of the recursive algorithm designed using the divide-and-conquer approach. Name the algorithm “MajEC”. Hint: divide the set of bank cards into two halves and call the algorithm recursively on each half.
3. [Run-time] Write a recurrence relation expressing the run-time T(n) of the recursive algorithm, and solve it to derive the run-time in big-O; it suffices to derive the closed functional form of the run-time and do not prove the big-O formally. The recurrence relation should have both recursive cases and base cases. Either the recursion tree technique or the telescoping technique can be used to derive the closed functional form. If the recurrence relation is one we have already solved in class, it is sufficient to refer to it without solving it again.

1. Property

Definining our theorem:

If there exists a majority equilvelance class in the set $S$ of size $n$, then at least one of the two halves

We seek to prove this by contradiction:

Let $S$ be a set of $n$ bank cars, such that there exists a majority equivalence class $C\in S$ , thus $|C|>\frac{n}{2}$.

Divide $S$ into two halves, $S_1$ and $S_2$ respectively. Each halve has a size of $\frac{n}{2}$ (assuming $n$ is even for simplicity, this can be extended to odd later)

For sake of contradiction, assume that neither $S_1,S_2$ contain majority equivalence class.

Meaning that every equivalence class in $S_1/S_2$ has size $\le \frac{n}{4}$ since majority requires $>\frac{n}{4}$.

Consider the cards of $C$ now, we let $c_1,c_2$ be the number of cards from $C$ in $S_1,S_2$ respectively.

Then, $c_1+c_2=|C|>\frac{n}{2}$. And since $C$ is an equivalence class, all its cards are equivalent to each other. Therefore $C\cap S_n$ forms an equivalence class in $S_n$, so $c_n\le \frac{n}{4}$ by our assumption ( where $n=\{1,2\}$).

We are left with:

$$|C|=c_1+c_2\le \frac{n}{4}+\frac{n}{4}=\frac{n}{2}$$

This contradics our initial premise that $|C|>\frac{n}{2}$, and thus our assumption is false and meaning that at least one of the two halves must contain a majority equivalence class $■$

2. Algorithm

see figure 4(might be on another page)

3. Run-time

We will perfomr a recurrence relation:

Let:

$$T(n)=\text{number of equivalence tests for a set of size }n$$

Our base cases are:

$$\begin{array}{r}T(0)=0\\ T(1)=0\\ T(2)=1\end{array}$$

And the recursive cases for $(n>2)$ are:

$$T(n)=T\left(\lfloor \frac{n}{2}\rfloor \right)+T\left(\lfloor \frac{n}{2}\rfloor \right)+cn$$

where:

• $cn$ represents the verification phase
• at most n tests for candidate1
• at most n tests for candidate2 (plus 1 test to check if candidates are equivalent)
• at most $2n+1$ tests in the combine step total

We can simplify this further:

$$T(n)=2T\left(\frac{n}{2}\right)+cn$$

for a constant c

Now we can solve:

$$\begin{array}{rlrl}\text{Level 0:}& cn& & \text{(1 node of size }n\text{)}\\ \text{Level 1:}& \frac{cn}{2}+\frac{cn}{2}=cn& & \text{(2 nodes of size }n/2\text{)}\\ \text{Level 2:}& \frac{cn}{4}+\frac{cn}{4}+\frac{cn}{4}+\frac{cn}{4}=cn& & \text{(4 nodes of size }n/4\text{)}\\ & ⋮& & \\ \text{Level }\log n:& cn& & \text{(}n\text{ nodes of size 1)}\end{array}$$

Num levels: ${\log }_{2}n+1$

work per level: $cn$

total work: $cn\cdot ({\log }_{2}n+1)=cn\log n+cn$

Thus:

$$T(n)=O(n\log n)$$