Weierstrass function

In the simplest terms, the Weierstrass function is a mathematical function that is continuous everywhere but differentiable nowhere. This means that while you can draw the function without lifting your pen from the paper, you cannot find a tangent line at any point on the curve.

---

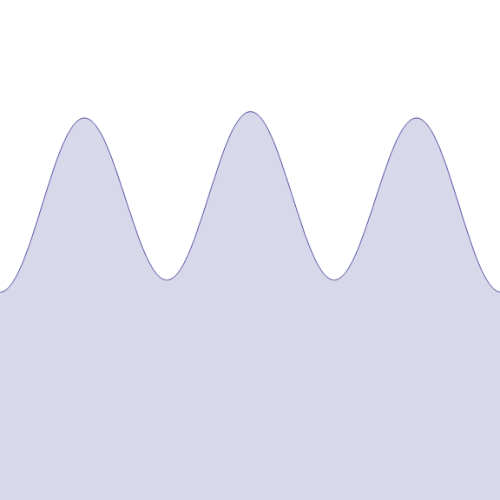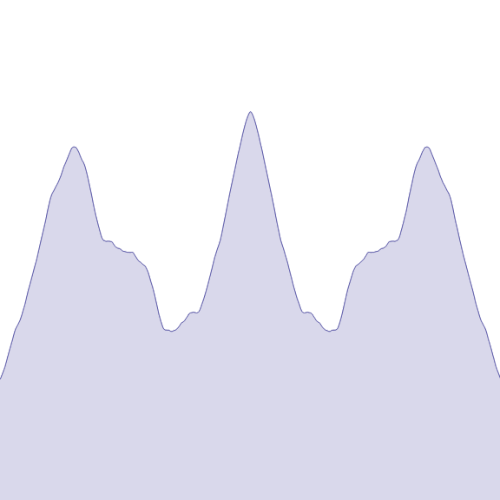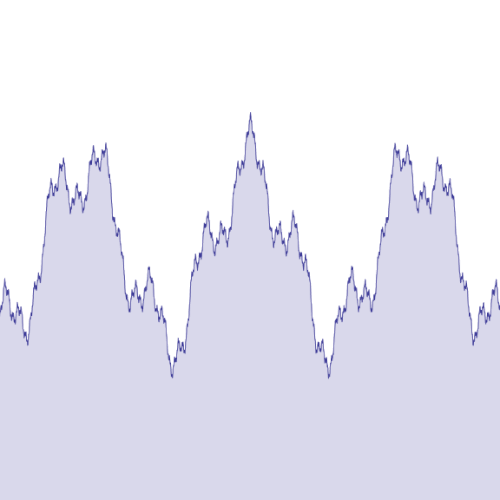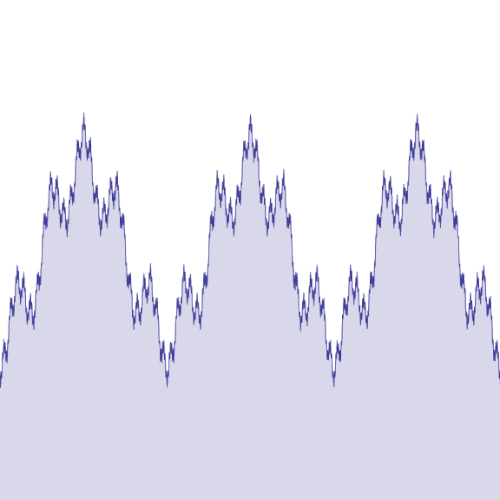
Formal Definition

Originally it was defined as the Fourier series:

$$W(x)=\sum _{n=0}^{\infty }{a}^n\cos (b^n\pi x).$$

where:

• $0<a<1$
• $b=\{2k+1|k\in \mathbb{N}\}$
• $ab>1+\frac{3}{2}\pi$

---

Properties

Beyond the obvious properties of being continuous everywhere and differentiable nowhere, the Weierstrass function has several other interesting properties.

Namely, it can be used to construct examples of functions that challenge our intuitive understanding of calculus and analysis. One of the most famous properties is that it is an example of a function that is continuous but not uniformly continuous.