Borsuk-Ulam Theorem

The Borsuk-Ulam Theorem states that for any continuous function mapping an $n$-dimensional sphere to ${\mathbb{R}}^n$, there exists a pair of antipodal points on the sphere that map to the same point in ${\mathbb{R}}^n$.

$$f:S^n\to {\mathbb{R}}^n$$

In plain english, in any dimensional sphere, there are always two opposite points that share the same property when mapped to a lower dimension.

THe most common example is the 2D sphere (the surface of the Earth). According to the Borsuk-Ulam Theorem, there are always two opposite points on the Earth’s surface that have the same temperature and pressure.

Another common one is The Stolen Necklace Problem, a discrete and seemingly unrelated problem regarding dividing a necklace with beads of different colors into two equal parts. The Borsuk-Ulam theorem can be used to prove that it is always possible to make such a division.

---

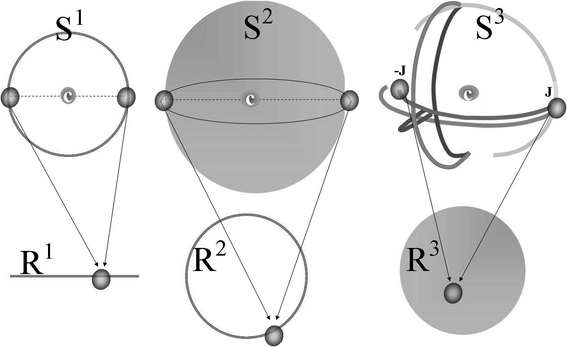
How We Know This

I don’t want to get into the actual proof of the theorem, but I want discuss how we know this is true.

Say there is a continuous function $f:S^n\to {\mathbb{R}}^n$ that does not have any Antipodal points that map to the same point in ${\mathbb{R}}^n$. This means that for every point $x$ on the sphere, $f(x)\ne f(-x)$.

Now, we can define a new function $g:S^n\to S^{n-1}$ that maps each point on the sphere to a point on the $(n-1)$-dimensional sphere. This function is defined as follows:

$$g(x)=\frac{f(x)-f(-x)}{\Vert f(x)-f(-x)\Vert }$$

At this point, we have a function that maps an $n$-dimensional sphere to an $(n-1)$-dimensional sphere. This is a contradiction, because it is known that there is no continuous function that can map an $n$-dimensional sphere to an $(n-1)$-dimensional sphere without identifying some points.