Hilbert Space

What is a Hilbert Space? David Hilbert and John von Neumann both played played key roles in the development of Hilbert Spaces, with Hilbert laying much of the groundwork and von Neumann finishing it off by giving the first complete definition of them. These spaces then quickly became useful in areas like Quantum Mechanics, the physics of heat transfer, and even modeling sound waves.

---

Let’s start with a simple vector. Imagine an arrow in the two dimensional plane. By choosing a specific coordinate system, we can specify the location of this vector with just two numbers: # of steps in x direction, and # of steps in y direction:

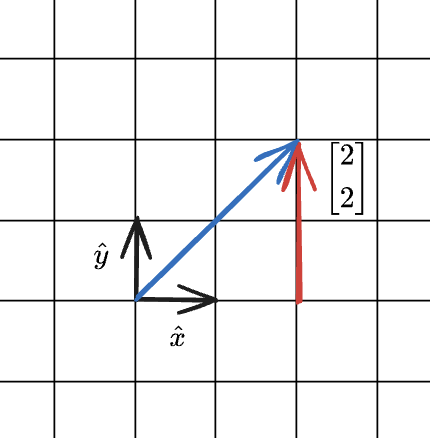
While this is generally the standard coordinate system used by all, there is nothing preventing us from using an alternative one.

We could just as easily use any other two vectors to form our coordinate system( so long as they have a $90^{\circ }$ angle between them ):

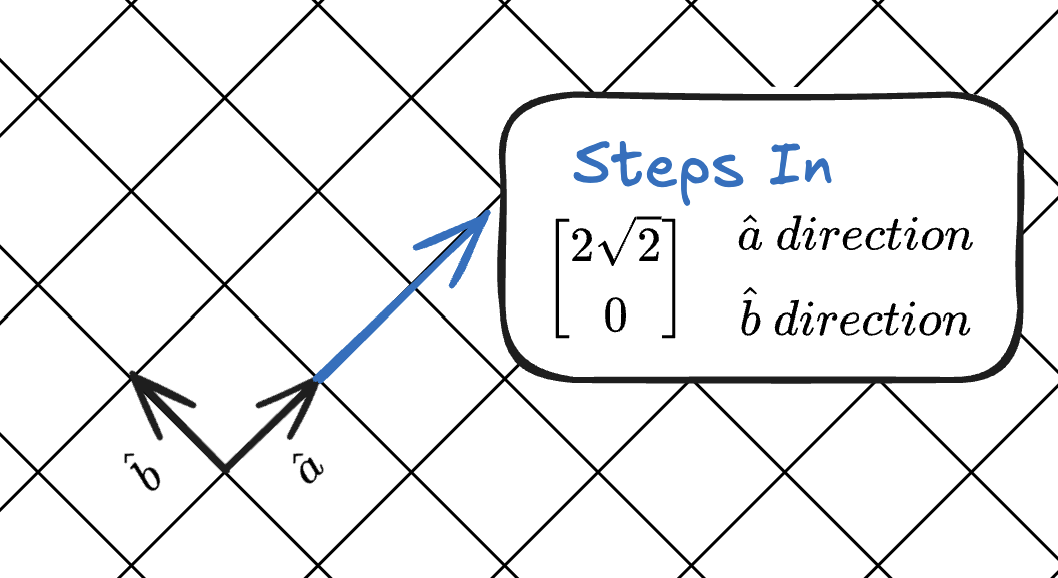
Within the field of Linear Algebra, we would say that these two vectors are Orthogonal to each other.

And, since any other vector in the plane can be expressed as some combination of these two vectors:

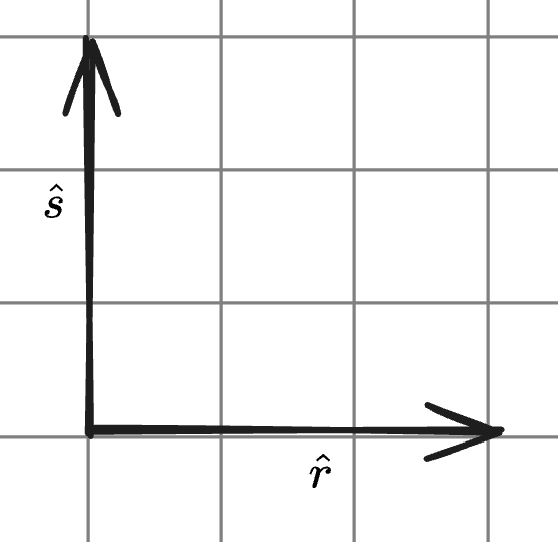
Then they form an orthogonal basis

$$\hat{r},\hat{s}\text{ form an orthogonal basis}$$

But if that these basis vectors also have a length of $1$, they would also form an orthonormal basis.

We will also be making use of the Dot Product of two vectors, but this is fairly known. (multiplies two vectors resulting in a single scalar value, evaluates the difference in direction between the two vectors):

$$Given:v_1=\left[\begin{array}{c}1\\ 3\end{array}\right],v_2=\left[\begin{array}{c}5\\ 2\end{array}\right]$$ $$\underset{\text{Dot Product}}{\underbrace{{\vec{v}}_1\cdot {\vec{v}}_2}}=(1\times 5)+(3\times 2)=11$$

One can see how this might be taken into the third dimension quite easily, and computing the dot product is still just as trivial. This can be scaled to any finite number of dimensions.

---

What a Hilbert Space is then, is the extension of these concepts to an infinite number of dimensions. And instead of just ordinary vectors as we know them ( arrows in space ), vectors in a Hilbert Space also include some abstract mathematical vectors.

These live in the Vector Space, which is a well-defined collection of objects that satisfy certain rules. Namely, you can scale and add vectors without leaving the space.

A lot of things can fall under this classification. For example:

• The set of all row vectors form a vector space.

$$\underset{\text{live in a n-dimensional vector space}}{\underbrace{[u_1,u_2,\dots ,u_n]}}$$

• So do the column vectors:

$$\underset{\text{live in a n-dimensional vector space}}{\underbrace{\left[\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_n\end{array}\right]}}$$

But also less conventional sets, like $n\times n$ matrices, and even functions also form a vector space.

Warning

Things get a little more abstract from this point forward, so always try to keep the 2-dimensional case in the back of your mind, that is the intuitive picture.

---

$$\cdots \leftarrow \{\text{actual hilber space stuff}\}$$