Infinity

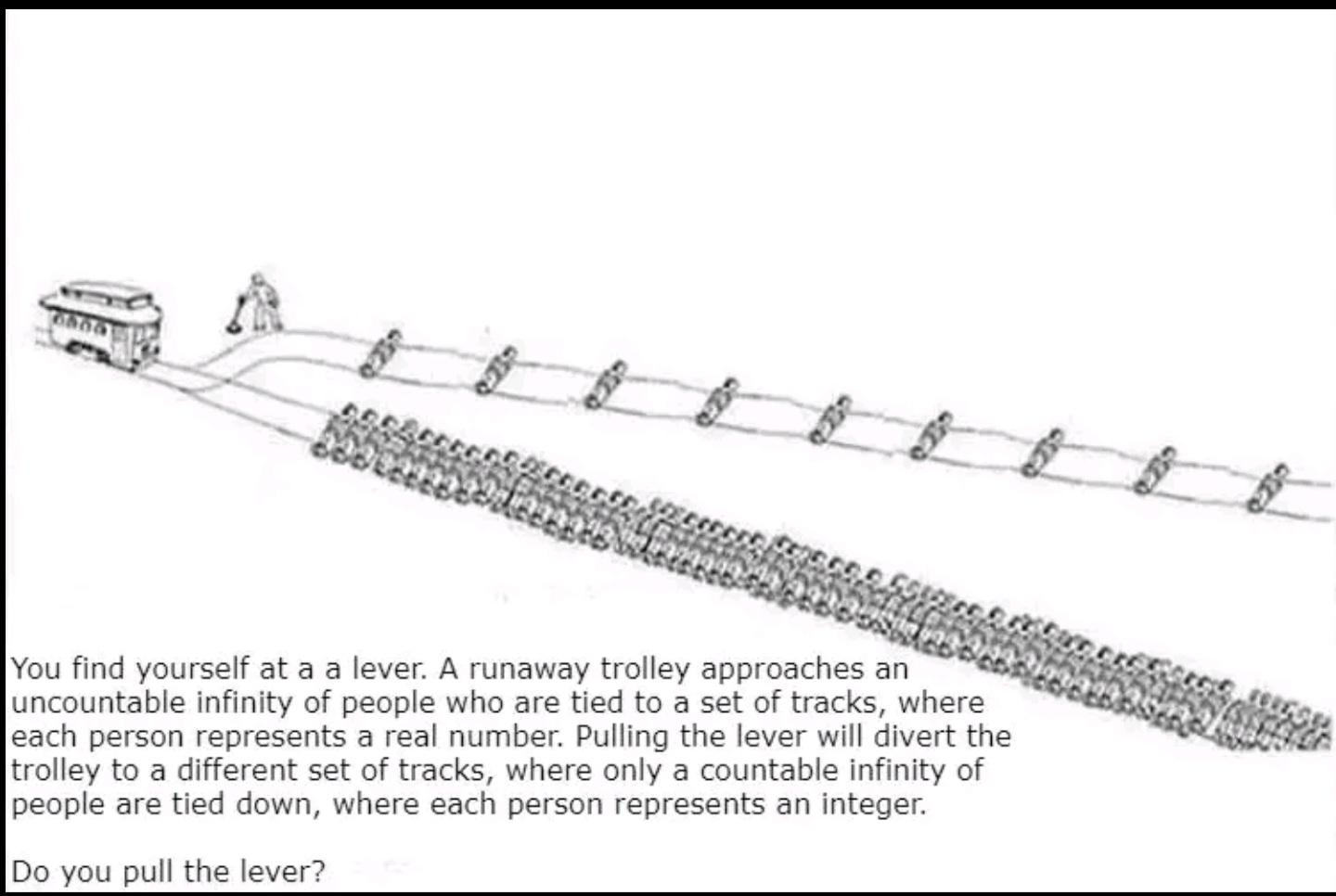
In set theory, infinity comes in different sizes. Countably infinite sets have cardinality $|\mathbb{N}|={\aleph }_0$ and can be listed in a sequence; see Countably Infinite. Uncountably infinite sets (like the reals) have cardinality $|\mathbb{R}|=2^{{\aleph }_0}=\mathfrak{c}>{\aleph }_0$; see Uncountably Infinite. The notion of size here is cardinality (equinumerosity up to bijection); see Cardinality.