The Cantor Set is a classic example of a set that is uncountably infinite, yet has measure zero. It is constructed by repeatedly removing the middle third of intervals, leading to a fractal structure.
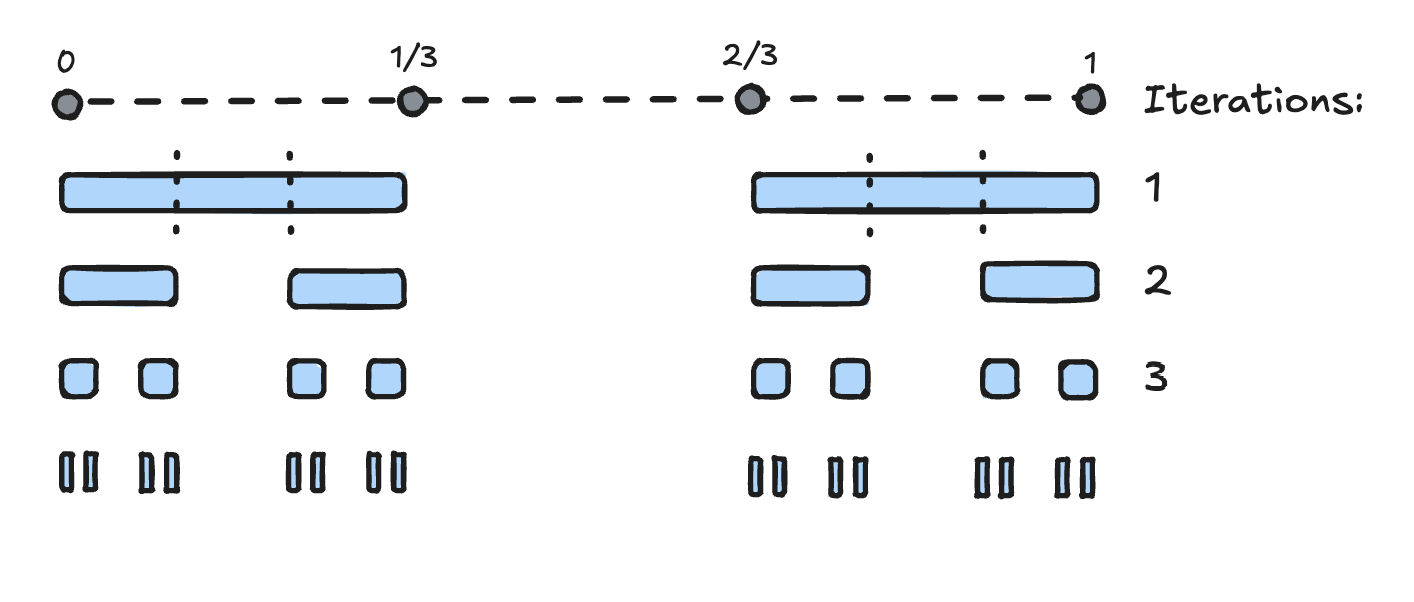
It is interesting in that it in of itself is a subset of the uncountably infinite set between and , but it is uncountably infinite in itself. It is also a perfect set, meaning it is closed and contains no isolated points. And yet, the area of the Cantor set is zero, as it is constructed by removing intervals of positive length.
It is defined as follows:
As follows, the Cantor set has a Cardinality equal to that of the Cardinality of the continuum, which is the Cardinality of all real numbers denoted .