Gaussian integers are complex numbers of the form where both and are integers. They form a ring, denoted by , which is the set of all Gaussian integers.
Not quite a complete ring, as it does not have a multiplicative identity (1 is not in the set). However, it is a subring of the complex numbers .
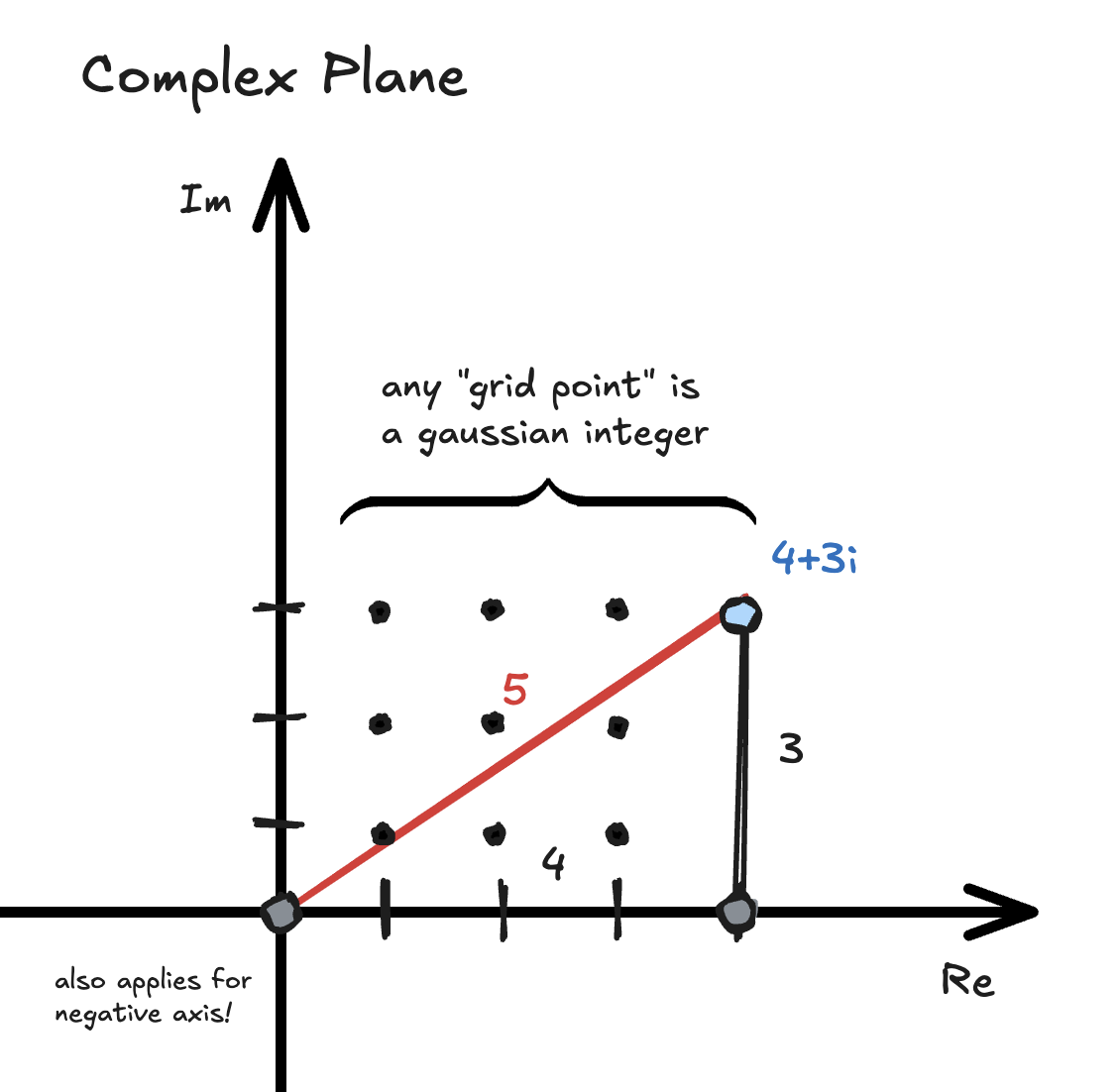
In the context of Gaussian integers, the term “lattice” refers to a discrete set of points in the complex plane that can be described by integer linear combinations of two basis vectors. In this case, the basis vectors are and , which correspond to the real and imaginary axes, respectively.
Think of the Gaussian integers as a two-dimensional lattice in the complex plane, where each point corresponds to a Gaussian integer. The real part corresponds to the x-axis and the imaginary part corresponds to the y-axis. It simply means that you can visualize Gaussian integers as the grid points in the complex plane.
An example where Gaussian integers are useful is in number theory, particularly in the study of Diophantine equations. For instance, the equation can be analyzed using Gaussian integers. If can be expressed as a product of Gaussian primes, it can provide insights into the solutions of the equation.
It is also well known in famous problems like finding the number of lattice points (Gaussian integers) that lie within a given circle in the complex plane. This is related to the distribution of prime numbers and has applications in various areas of mathematics, including algebraic number theory and cryptography.