Normalization, Regularization, and Gradient Descent for Linear Regression

As we discussed last lecture on Linear and Nonlinear Regression, for the case of linear regression we can solve the parameters with a closed form solution. But, to introduce the concept of Gradient Descent, we must build an intuition of the process.

---

Approach

We start by initializing $\theta$ parameters, usually either zeros or just randomly set.

Then given the gradient of our Loss Function, we are looking to find the direction of fastest descent. Then we update our parameters in that direction scaled by a learning rate $\eta$. This all comes together in the partial derivative of the loss function with respect to each parameter ${\theta }_j$. If not familiar, I recommend reviewing Partial Derivatives, Vector Fields, and maybe 14.6 - Directional Derivatives.

We repeat until convergence ${\theta }_j^{new}\leftarrow {\theta }_j^{old}-\eta \frac{\partial }{\partial {\theta }_j}L(\theta )$. This is called Batch Gradient Descent since we are using the entire dataset to compute the gradient at each step.

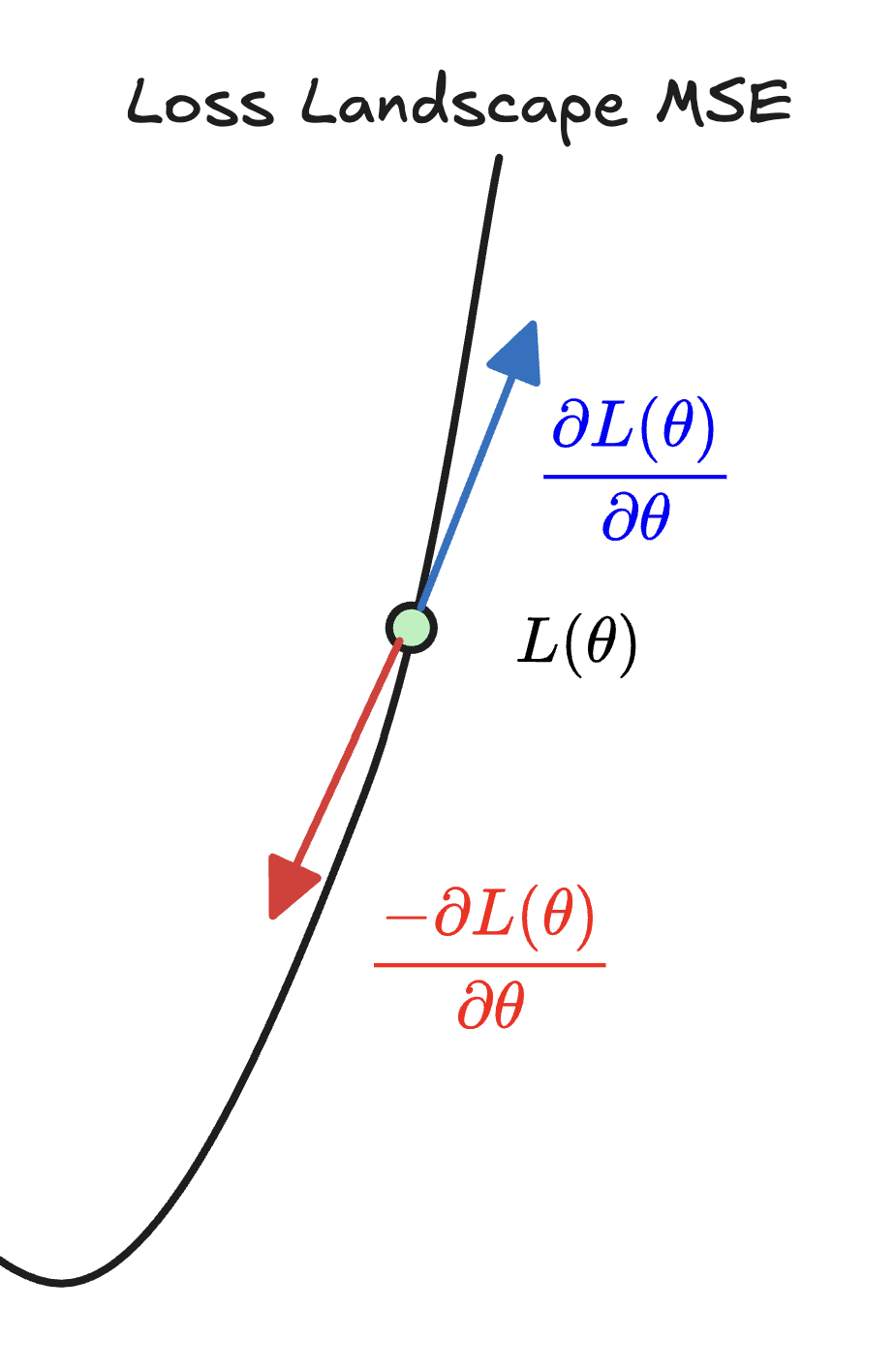
Gradient Descent Variations

A few ones to be aware of:

1. Batch Gradient Descent: As described above, uses the entire dataset to compute the gradient at each step. This can be computationally expensive for large datasets.
2. Stochastic Gradient Descent (SGD): Instead of using the entire dataset, SGD updates the parameters using only one training example at a time. This can lead to faster convergence but introduces more noise in the updates.
3. Mini-Batch Gradient Descent: A compromise between batch and stochastic gradient descent

To help mini-bath GF and SGF to reach the topimal solution, gradually reduce the learning rate $\eta$ by factor of 0.9 every epoch.

Feature Scaling

If features are different in sizes/scales. For example, one feature is in the range of 1-10 while another is in the range of 1-1000. This can cause the gradient descent to converge slowly or even diverge.

First approach is Normalization, where you rescale the features to a standard range, typically [0, 1]. This can be done using the formula:

$$x^{\prime }=\frac{x-x_{min}}{x_{max}-x_{min}}$$

There are several kinds of normalization, this is called Min-Max Normalization. There is also mean normalization, where you subtract the mean and divide by the range.

---

Non Linear Regression

What if your data is more complex than a straight line?

Can we use a linera model to fit it? Yah, but wont fit well.

How can we fix? We can add powers of features to create a polynomial regression model.

Polynomial regression can fit just about any curve, but be careful of overfitting. Use cross validation to select the right degree of polynomial.

This is what is used in Taylor Series approximations, but this time for regression. Polynomials in this case will look something like:

$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+...+{\theta }_n{x}^n$$

---

Regularization

Regularization is a technique used to prevent overfitting in machine learning models by adding a penalty term to the loss function. This penalty discourages the model from fitting the noise in the training data, leading to better generalization on unseen data.

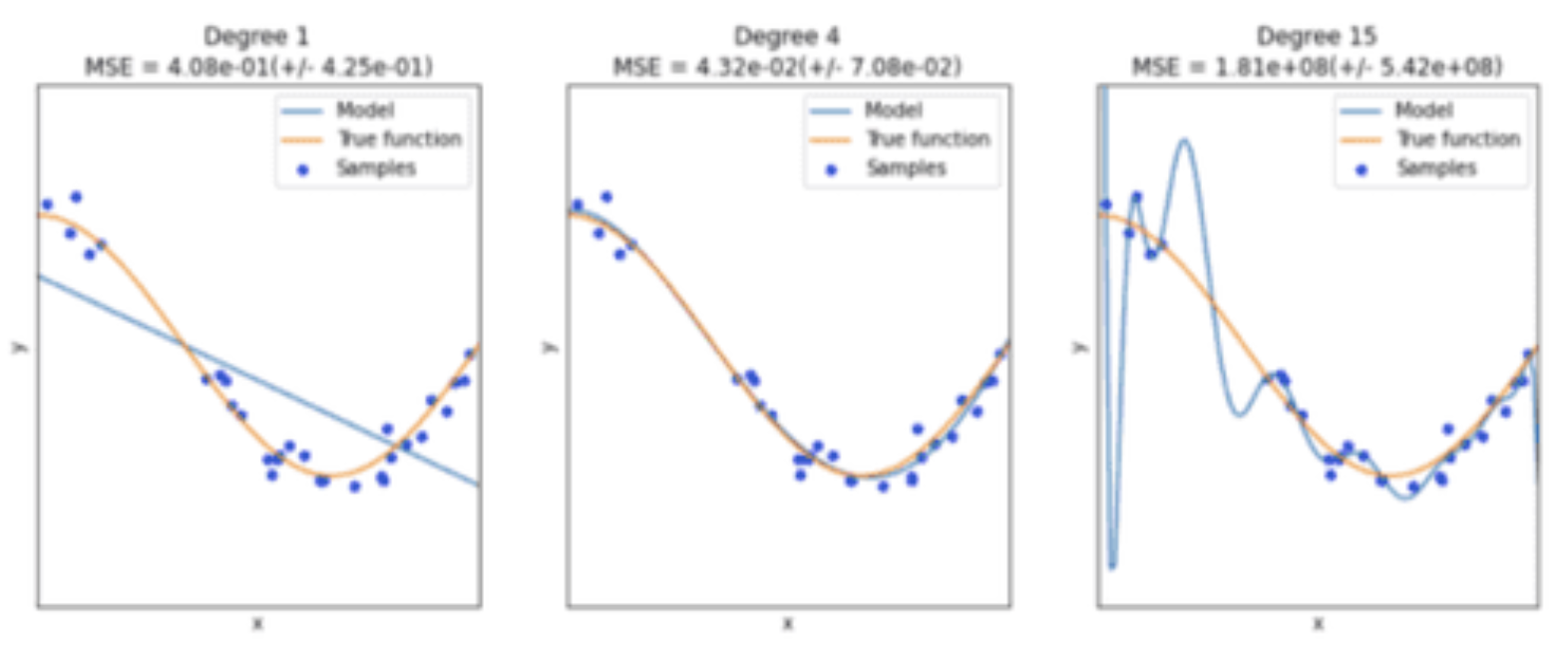
Noise is proprtional to model complexity. The more complex the model, the more it can fit noise.

Ridge Regression

Taking the our previous loss function for linear regression, we can add a regularization term to penalize large weights. This helps to prevent overfitting by discouraging complex models.

$$J(\theta )=\frac{1}{m}\sum _{i=0}^m(h_{\theta }(x^i)-y^i{)}^2$$

Adding regularization term:

$$J(\theta )=\frac{1}{m}\sum _{i=0}^m(h_{\theta }(x^i)-y^i{)}^2+\frac{\alpha 1}{2}\sum _{i=1}^n{\theta }_i^2$$

Simplifying:

$$J(\theta )=MSE(\theta )+\alpha \cdot \frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$

Where:

• ${\theta }_i$ is the feature weight
• $\alpha$ controls how much you want to regularize the model. we call it Regularization Rate. It is multiplied by 1/2 for mathematical convenience when taking derivatives.
• $\alpha =0$ means no regularization

In gradient descent, the cost function changes to:

$$MSE(\vec{\theta })+\frac{\alpha }{2}\sum _{j=1}^n{\theta }_j^2$$

Yielding:

$$\Rightarrow \frac{\partial J}{\partial {\theta }_j}=\frac{2}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i+\alpha {\theta }_j$$

Lasso Regression

Lasso regression is another regularization technique that adds a penalty term to the loss function, but instead of using the square of the weights, it uses the absolute value of the weights. This can lead to sparse models where some weights are exactly zero, effectively performing feature selection.

$$J(\theta )=MSE(\theta )+\alpha \cdot \sum _{j=1}^n|{\theta }_j|$$

Elastic Net

Elastic Net combines both Ridge and Lasso regression by adding both penalty terms to the loss function. This can provide a balance between the two methods and can be particularly useful when dealing with correlated features.

$$J(\theta )=MSE(\theta )+{\alpha }_1\cdot \frac{1}{2}\sum _{j=1}^n{\theta }_j^2+{\alpha }_2\cdot \sum _{j=1}^n|{\theta }_j|$$

When to Use What?

It is almost always prefereable to have at least a little bit of regularization to prevent overfitting, especially with complex models.

Elastic net is a middle ground betwen ridge regression and Lasso Regression. Use ridge when all features are relevant, Lasso when you want feature selection, and elastic net when you want a balance of both.

Maybe start wtih elastic net and tune the hyperparameters ${\alpha }_1$ and ${\alpha }_2$ using cross-validation to find the best balance for your specific problem. Then try ridge and Lasso to see if they perform better.