Hilbert Transform

The Hilbert Transform is a tool for signal processing that allows us to convert a real valued signal into its analytic representation, which is a complex-valued signal. This transformation is particularly useful for extracting instantaneous amplitude and phase information from oscillatory signals, such as neural signals in computational neuroscience.

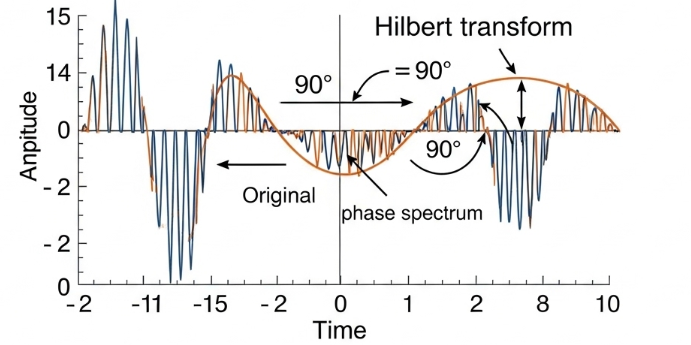
In layman’s terms, it is a filter that leaves the amplutude of each frequency component unchanged but shifts the phase of each component by 90 degrees. This phase shift allows us to construct a complex signal where the real part is the original signal and the imaginary part is the Hilbert transform of the original signal.

---

Intuition

The goal of the Hilbert Transform is to create its Analytic Signal. For real world signals like EEG data, it can be usefull to imagine them as rotating Phasors in the complex plane, allowing us to track how their amplitude and phase change over each moment.

Given a real signal $x(t)$, its analytic signal $z(t)$ is defined as:

$$z(t)=x(t)+j\cdot \mathcal{H}[x(t)]$$

Where:

• $x(t)$ is the original real-valued signal.
• $\mathcal{H}[x(t)]$ is the Hilbert Transform of $x(t)$.
• $j$ is the imaginary unit

With this analytic signal, we can compute the Instantaneous Amplitude and Instantaneous Phase.

The Instantaneous Amplitude $A(t)$ can be calculated by taking the magnitude of the complex vector $|z(t)|$. This traces the outline as seen in the above image.

The Instantaneous Phase $\varphi (t)$ can be calculated using the arctangent of the ratio of the imaginary part to the real part of the analytic signal $\angle z(t)$. The derivative of this phase with respect to time gives us the Instantaneous Frequency.

Formulation

There exists two definitions of the Hilbert Transform, one in the time domain and one in the frequency domain.

Time Domain

We convolute the signal $x(t)$ with the function $\frac{1}{\pi t}$. Defined formally using the Cauchy principal value, the Hilbert Transform $\mathcal{H}[x(t)]$ is given by:

$$\mathcal{H}[x(t)]=\frac{1}{\pi }\text{P.V.}{\int }_{-\infty }^{\infty }\frac{x(\tau )}{t-\tau }d\tau$$

Revealing the local symmetry of the signal around each point in time.

Frequency Domain

This version is much more intuitive. The Hilbert Transform can be understood in terms of its effect on the frequency components of the signal. In the frequency domain, the Hilbert Transform is defined by multiplying the Fourier Transform of the signal $X(f)$ by $-j\cdot \text{sgn}(f)$, where $\text{sgn}(f)$ is the sign function.

$$\mathcal{F}\{\mathcal{H}[x(t)]\}=-j\cdot \text{sgn}(f)\cdot X(\omega )$$

Defining the $sgn(\omega )$ function more explicitly:

For Positive Frequencies ($\omega >0$): Multiply by $-j$ (phase shift of -90 degrees)

For Negative Frequencies ($\omega <0$): Multiply by $+j$ (phase shift of +90 degrees)

And the DC Component ($\omega =0$): Multiply by $0$ (removes the DC component)

---

Example

A simple example with trig functions for a cosine wave:

$$x(t)=\cos (\omega t)$$

Hilbert Transform shifts it by 90 degrees to become a sine wave:

$$\mathcal{H}[\cos (\omega t)]=\sin (\omega t)$$

Yielding the analytic signal:

$$z(t)=\cos (\omega t)+j\sin (\omega t)=e^{j\omega t}$$

Where its envelope (instantaneous amplitude) is constant at $|e^{j\omega t}|=1$, and its instantaneous phase increases linearly over time.

And it’s easy to see that the instantaneous frequency is simply $\omega t$, linear growth over time.

---

Implementation

Python

Output