Assignment 5

Problem 1

Question

Let $f:\mathbb{R}\to \mathbb{R}$ be a continuous, differentiable map. Assume $0$ is a sink and $(-1,1)$ is the largest interval that lies entirely inside the basin of $0$. The points $1$ and $-1$ are not in the basin of $0$.

(a) What are the possible trajectories of the points $-1$ and $1$?

(b) What are the possible Lyapunov numbers for each of $-1$, $0$, $1$?

A

$(-1,1)$ is the max interval for $0$‘s basin. $f(\pm 1)\notin (-1,1)$.

by contradiction: suppose $f(-1)\in (-1,1)$. then $f^n(f(-1))\to 0$, so $f^{n+1}(-1)\to 0$, putting $-1$ in the basin. impossible! so $|f(-1)|\ge 1$. same for $1$.

since orbit of $-1$ (resp. $1$) can never enter $(-1,1)$, our possible trajectories are:

• fixed: $f(-1)=-1$ or $f(1)=1$
• period-2: $f(-1)=1$ and $f(1)=-1$
• eventually fixed: one maps to the other which is fixed, say $f(1)=-1$ where $f(-1)=-1$
• divergent: orbit escapes to $\pm \infty$

Answer

both $-1$ and $1$ must map outside $(-1,1)$ since orbits either settle to fixed/periodic on boundary, or will diverge.

B

Lyapunov Number: $L(x_0)={\lim }_{n\to \infty }|f^{\prime }(x_0)\cdot f^{\prime }(x_1)\cdots f^{\prime }(x_{n-1}){|}^{1/n}$

for $0$: fixed point, orbit is $\{0,0,\dots \}$. so:

$$L(0)=|f^{\prime }(0)|$$

$0$ is a sink implying $|f^{\prime }(0)|<1$, so $L(0)\in [0,1)$.

for $-1$ and $1$: suppose $L(-1)<1$. then orbit of $-1$ converges to some attracting set $\gamma$. the basin of $\gamma$ is open, so it contains a neighborhood $(-1-ϵ,-1+ϵ)$. but $(-1,-1+ϵ)\subset$ basin of $0$, meaning those points converge to $0\ne \gamma$. impossible! contradiction

same argument for $1$.

Answer

• $L(0)=|f^{\prime }(0)|\in [0,1)$
• $L(-1)\ge 1$
• $L(1)\ge 1$

equality $L=1$ if boundary points neutral, $L>1$ if repelling or divergent.

---

Problem 2

Question

Show that if the Lyapunov number of the orbit of $x_0$ under $f$ is $L$, then the Lyapunov number of the orbit of $x_0$ under $f^k$ is $L^k$, whether or not $x_0$ is periodic. Note that if the orbit of $x_0$ under $f$ is $\{x_0,x_1,x_2,\dots \}$ then the orbit under $f^k$ is $\{x_0,x_k,x_{2k},x_{3k},\dots \}$.

lyapunov number for $x_0$ under $f$:

$$L=\underset{n\to \infty }{\lim }|f^{\prime }(x_0)\cdot f^{\prime }(x_1)\cdots f^{\prime }(x_{n-1}){|}^{1/n}$$

orbit $x_0$ under $f^k$ : $\{x_0,x_k,x_{2k},\dots \}$. lyapunov number under $f^k$:

$$L_{f^k}=\underset{m\to \infty }{\lim }|(f^k{)}^{\prime }(x_0)\cdot (f^k{)}^{\prime }(x_k)\cdots (f^k{)}^{\prime }(x_{(m-1)k}){|}^{1/m}$$

chain rule yields

$$(f^k{)}^{\prime }(x_{jk})\approx \prod _{i=0}^{k-1}{f}^{\prime }(x_{jk+i})$$

so the product over $m$ terms of $f^k$ unfolds into the product over $mk$ terms of $f$:

$$\prod _{j=0}^{m-1}(f^k{)}^{\prime }(x_{jk})=\prod _{j=0}^{m-1}\prod _{i=0}^{k-1}{f}^{\prime }(x_{jk+i})=\prod _{\ell =0}^{mk-1}{f}^{\prime }(x_{\ell })$$

substituting:

$$L_{f^k}=\underset{m\to \infty }{\lim }{\left|\prod _{\ell =0}^{mk-1}{f}^{\prime }(x_{\ell })\right|}^{1/m}=\underset{m\to \infty }{\lim }{\left|\prod _{\ell =0}^{mk-1}{f}^{\prime }(x_{\ell })\right|}^{k/(mk)}$$

set $n=mk$. since $L$ exists, limit along sub sequence $n=mk\to \infty$ is $L$:

$$L_{f^k}={\left(\underset{n\to \infty }{\lim }{\left|\prod _{\ell =0}^{n-1}{f}^{\prime }(x_{\ell })\right|}^{1/n}\right)}^k=L^k$$

Answer

$L_{f^k}=L^k$. the chain rule collapses the $f^k$ product into the $f$ product, and the $1/m$ exponent becomes $k/n$, pulling out the $k$th power.

---

Problem 3

Question

Begin by sketching $g(x)=2.5x(1-x)$ and considering cobweb plots of typical orbits.

(a) What are the possible bounded asymptotic behaviors for all $x\in \mathbb{R}$?

(b) Find the Lyapunov exponent shared by most bounded orbits of $g(x)$.

(c) Do all bounded orbits have the same Lyapunov exponent?

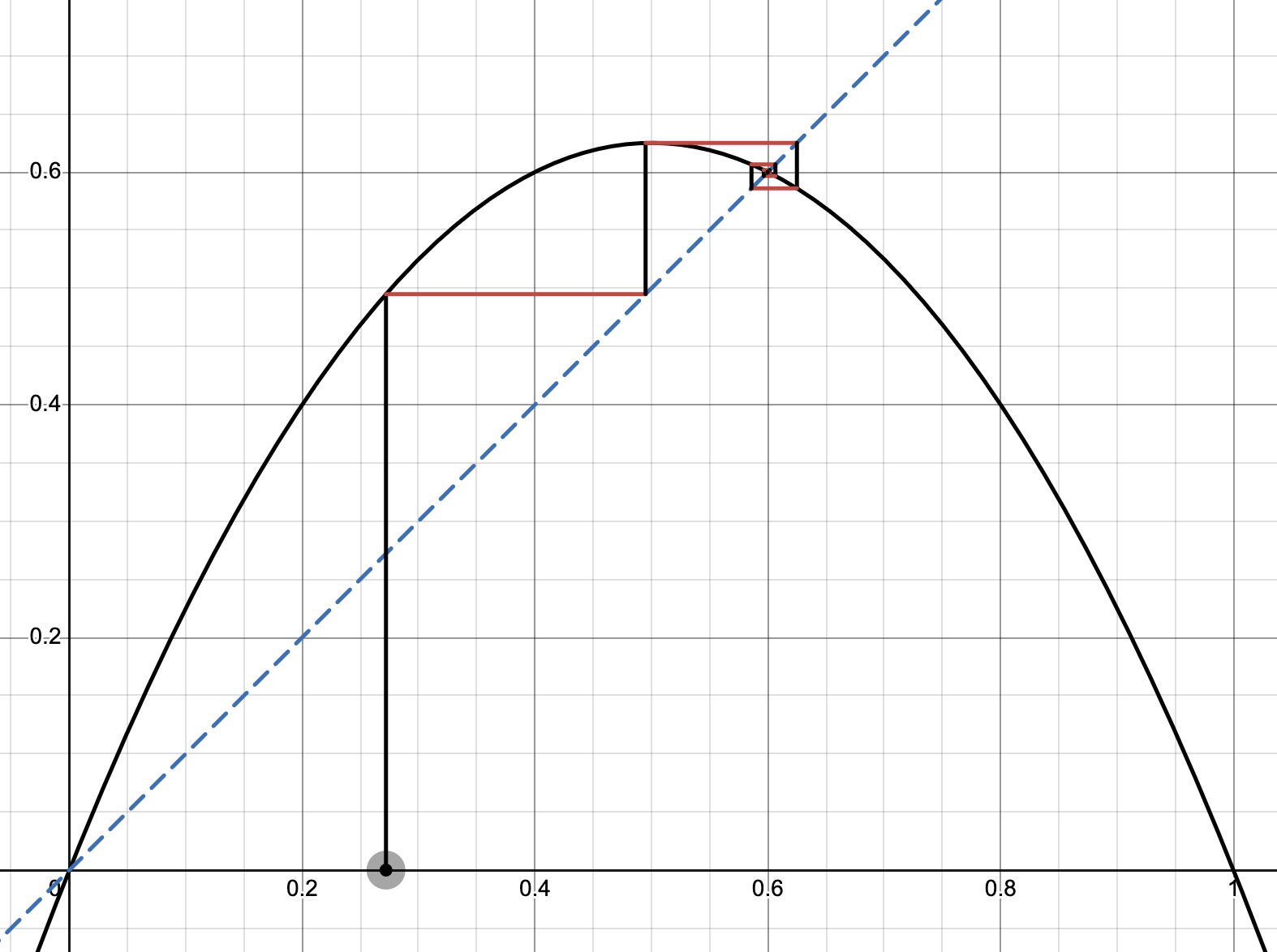
$g(x)=2.5x(1-x)$. Logistic Map variant, vertex at $(0.5,0.625)$, roots at $0$ and $1$ maps $[0,1]\to [0,0.625]\subset [0,1]$.

$g^{\prime }(x)=2.5-5x$.

fixed points$g(x)=x$:

$$2.5x(1-x)=x⟹x(1.5-2.5x)=0$$

so $x=0$ and $x=3/5$.

stability:

$g^{\prime }(0)=2.5>1$ is repelling, - $g^{\prime }(3/5)=2.5-3=-0.5$, $|-0.5|<1$ is attracting

since $a=2.5<3$, were below first period- doubling bifrication. no periodic orbits exist beyond fixed points.

A

for $x\in (0,1)$: cobweb spirals into $x^{\ast }=3/5$ (negative derivative yields alt approach). every orbit in $(0,1)\setminus \{0\}$ converges to $3/5$.

for $x\notin [0,1]$: if $x>1$, then $g(x)=2.5x(1-x)<0$. if $x<0$, then $|g(x)|=2.5|x|(1+|x|)>2.5|x|$, so iterates grow without bound. orbits diverge to $-\infty$.

Answer

bounded asymptotic behaviors:

1. convergence to attracting fixed point $x^{\ast }=3/5$ (generic — all of $(0,1)\setminus \{0\}$)
2. fixed at $x=0$ only repelling at exactly 0
3. eventually fixed at $0$ ($x=1\to 0\to 0\to \cdots$)

B

most bounded orbits converge to $x^{\ast }=3/5$. once near the fixed point, $g^{\prime }(x_n)\to g^{\prime }(3/5)=-1/2$, so:

$$\lambda =\underset{n\to \infty }{\lim }\frac{1}{n}\sum _{i=0}^{n-1}\ln |g^{\prime }(x_i)|=\ln |g^{\prime }(3/5)|=\ln \frac{1}{2}$$

Answer

$\lambda =-\ln 2\approx -0.693$

C

no. the repelling fixed point $x=0$ has:

$$\lambda (0)=\ln |g^{\prime }(0)|=\ln (5/2)\approx 0.916>0$$

and $x=1$ eventually maps to $0$, so its lyapunov exponent is also $\ln (5/2)$.

Answer

not all bounded orbits share the same exponent. the measure-zero set $\{0,1\}$ has $\lambda =\ln (5/2)>0$, while the generic orbit has $\lambda =-\ln 2<0$.

---

Problem 4

Question

Begin by sketching $g(x)=2-x^2$ and considering cobweb plots of typical orbits.

(a) Find a conjugacy $C$ between $G(x)=4x(1-x)$ and $g$.

(b) Use the conjugacy to find the fixed points and period-2 orbits of $g$ (if they exist) and determine their stability.

(c) Show that $g$ has chaotic orbits.

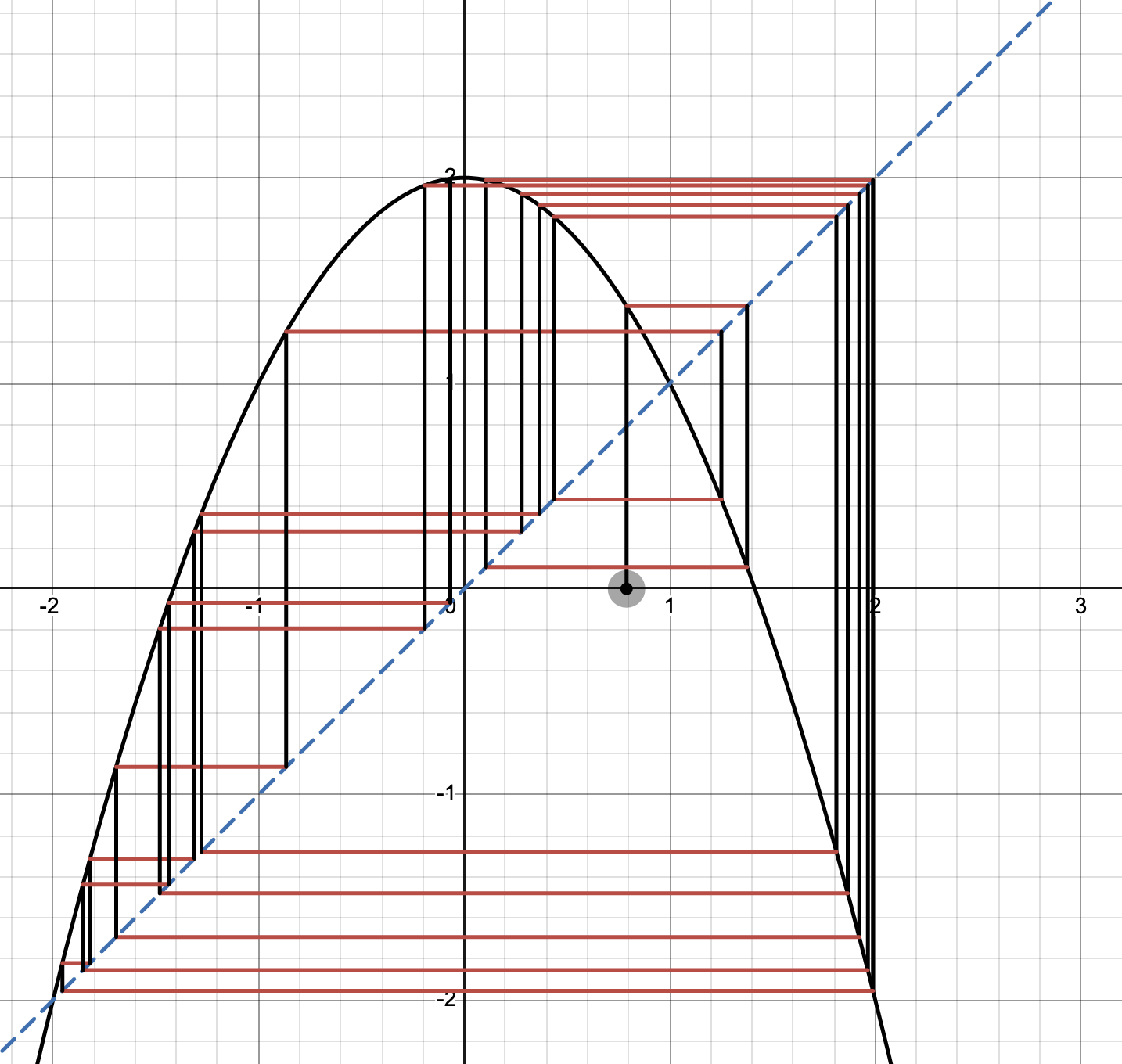
$g(x)=2-x^2$. downward parabola, vertex at $(0,2)$, roots at $\pm \sqrt{2}$. desmos graph shows chaotic behavior everywhere except 1 ( on rough explorations ). Bounded between -2 and 2.

A

want $C$ such that $C\circ G=g\circ C$. try affine $C(x)=\alpha x+\beta$.

$$C(G(x))=\alpha \cdot 4x(1-x)+\beta =-4\alpha x^2+4\alpha x+\beta$$ $$g(C(x))=2-(\alpha x+\beta {)}^2=-{\alpha }^2{x}^2-2\alpha \beta x+2-{\beta }^2$$

matching coefficients:

$x^2$: $-4\alpha =-{\alpha }^2⟹\alpha =4$

$x^1$: $4\alpha =-2\alpha \beta ⟹16=-8\beta ⟹\beta =-2$

$x^0$: $\beta =2-{\beta }^2⟹-2=2-4=-2$ ✓

Answer

$C(x)=4x-2$, maps $[0,1]\to [-2,2]$.

B

fixed points of $G$: $4x(1-x)=x⟹x(3-4x)=0$, so $x=0$ and $x=3/4$.

map through conjugacy:

• $C(0)=-2$ → $g(-2)=2-4=-2$ - yes
• $C(3/4)=1$ → $g(1)=2-1=1$ - yes

stability via $g^{\prime }(x)=-2x$:

• $g^{\prime }(-2)=4$, $|g^{\prime }|=4>1$ - repelling
• $g^{\prime }(1)=-2$, $|g^{\prime }|=2>1$ - repelling

period-2 orbits of $G$: fixed points of $G^2$ minus fixed points of $G$. setting $G^2(x)=x$ and factoring out the known roots:

$$64x^3-128x^2+80x-15=(4x-3)(16x^2-20x+5)=0$$

period-2 points from the quadratic:

$$x=\frac{5\pm \sqrt{5}}{8}$$

map through conjugacy:

$$C\left(\frac{5\pm \sqrt{5}}{8}\right)=\frac{5\pm \sqrt{5}}{2}-2=\frac{1\pm \sqrt{5}}{2}$$

so the period-2 orbit of $g$ is $\left\{\frac{1+\sqrt{5}}{2},\frac{1-\sqrt{5}}{2}\right\}$ — the golden ratio and its conjugate.

verify: $g(\varphi )=2-{\varphi }^2=2-(\varphi +1)=1-\varphi$ ✓ (using ${\varphi }^2=\varphi +1$).

stability:

$$(g^2{)}^{\prime }=g^{\prime }(\varphi )\cdot g^{\prime }(1-\varphi )=(-(1+\sqrt{5}))(\sqrt{5}-1)=-(5-1)=-4$$

$|(g^2{)}^{\prime }|=4>1$ → repelling.

Answer

fixed points: $-2$ (repelling), $1$ (repelling). period-2 orbit: $\{\varphi ,1-\varphi \}$ (repelling). all periodic orbits are unstable.

C

$C(x)=4x-2$ is affine, so $C^{\prime }=4$ everywhere. from the conjugacy relation:

$$C^{\prime }(G(x))\cdot G^{\prime }(x)=g^{\prime }(C(x))\cdot C^{\prime }(x)⟹G^{\prime }(x)=g^{\prime }(C(x))$$

derivatives along corresponding orbits are identical. so lyapunov exponents are preserved exactly.

$G(x)=4x(1-x)$ is chaotic on $[0,1]$: has orbits of every period (HW4 Problem 1), lyapunov exponent $\lambda =\ln 2>0$ for almost every orbit.

since $C$ is a topological conjugacy preserving sensitive dependence, dense periodic orbits, and transitivity:

Answer

$g$ is chaotic on $[-2,2]$. conjugacy to $G$ gives $\lambda =\ln 2>0$ (sensitive dependence) and periodic orbits of every period. the cobweb had this visually with never settling orbits

---

Problem 5

Question

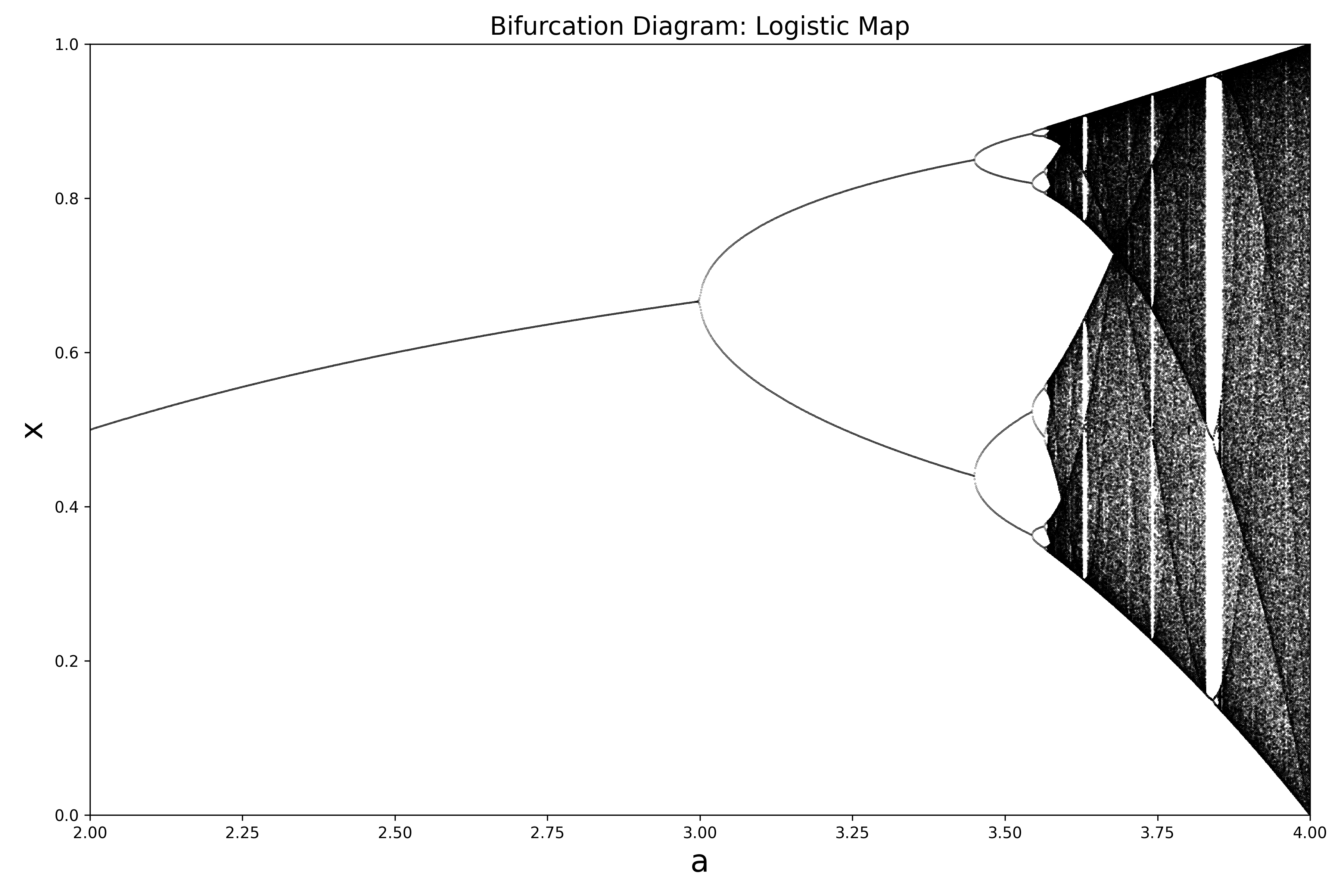
(a) Write a program to draw the bifurcation diagram for the logistic map $g_a(x)=ax(1-x)$ for $a\in [2,4]$ in increments of $0.001$. Iterate $1000$ times from a random $x_0\in (0,1)$. Plot the bifurcation diagram.

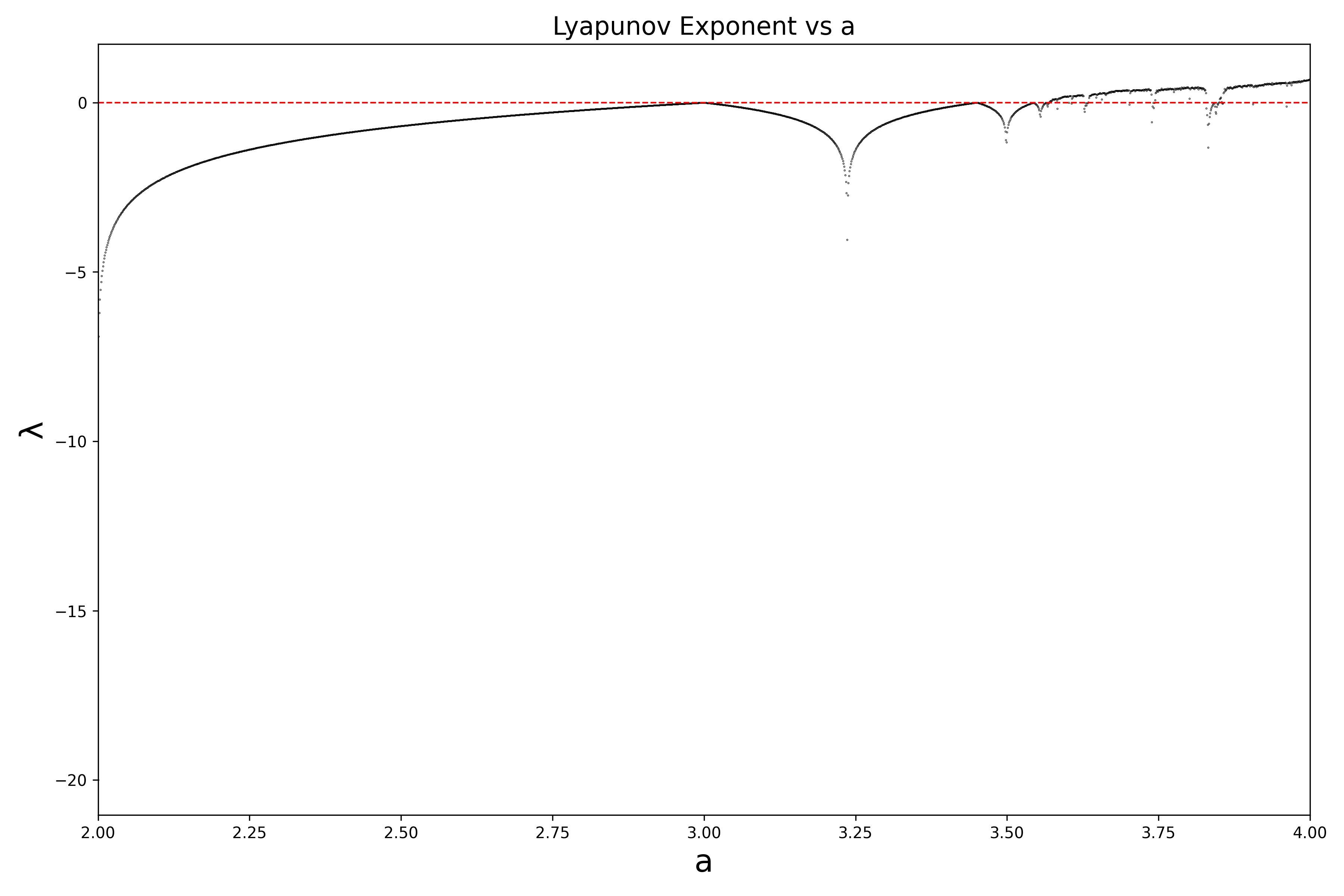
(b) Use iterates 101 to 1000 to approximate the Lyapunov exponent for each $a$. Graph $\lambda$ vs $a$ with a horizontal line at $0$.

(c) What do you learn from comparing the two pictures?

(d) Why does the Lyapunov exponent appear to bounce off zero several times before becoming positive?

(e) Will a new random $x_0$ produce the same figure? Why or why not?

C

two figures show that where $\lambda <0$, bifurcation diagram yields clean bands (stable periodic orbits). where $\lambda >0$, diagram shows dense chaotic scatter. $\lambda$ crosses zero exactly at bifurcation points where stability is lost.

periodic windows in the chaotic regime (e.g. the period-3 window near $a\approx 3.83$) show up as sharp dips of $\lambda$ below zero in the lyapunov plot.

the lyapunov exponent is quantitative version of what bifurcation diagram suggests: $\lambda <0$ = order, $\lambda >0$ = chaos.

D

each “bounce” off zero is a period-doubling bifurcation. at the bifurcation point, the eigenvalue of the periodic orbit passes through $-1$, so $|(g^k{)}^{\prime }|=1$ and $\lambda =0$.

between successive bifurcations, the new orbit is stable ($\lambda <0$). as $a$ increases, back to $0$ for next doubling. bounces get closer together (feigenbaum scaling) until accumulation point $a_{\infty }\approx 3.5699\dots$ where chaos begins, $\lambda$ crosses above zero.

E

yes, a new random $x_0\in (0,1)$ produces the same figure. the logistic map has a unique attractor for each $a$, and almost every orbit converges to it regardless of initial condition. the lyapunov exponent is also identical for most $x_0$

only exceptions are measure-zero sets, in that, exact unstable periodic points / their pre imgs. random $x_0$ hits these with zero probability.

Cod

Python

import numpy as np import matplotlib.pyplot as plt N = 1000 amin, amax, da = 2.0, 4.0, 0.001 x0 = np.random.random() # bif diagram a_vals, x_plot = [], [] for a in np.arange(amin, amax + da/2, da): x = np.zeros(N + 1) x[0] = x0 for i in range(N): x[i+1] = a * x[i] * (1 - x[i]) # periods S = 9 p = S for j in range(S + 1): if abs(x[-1] - x[-1 - 2**j]) < 1e-5: p = j break pts = x[-(2**p):] a_vals.extend([a] * len(pts)) x_plot.extend(pts) plt.figure(figsize=(12, 8)) plt.scatter(a_vals, x_plot, c='k', s=0.1, marker='.') plt.xlabel('a', fontsize=20); plt.ylabel('x', fontsize=20) plt.title('Bifurcation Diagram: Logistic Map', fontsize=16) plt.xlim([2, 4]); plt.ylim([0, 1]) plt.tight_layout() plt.savefig('p5_bifurcation.png', dpi=300) plt.close() # lyapunov exponent a_range = np.arange(amin, amax + da/2, da) lyap = np.zeros(len(a_range)) for idx, a in enumerate(a_range): x = np.zeros(N + 1) x[0] = x0 for i in range(N): x[i+1] = a * x[i] * (1 - x[i]) # g'(x) = a(1 - 2x) # iterates 101-1000 derivs = np.abs(a * (1 - 2 * x[100:1000])) derivs = derivs[derivs > 0] # no log 0 lyap[idx] = np.mean(np.log(derivs)) if len(derivs) > 0 else -20 plt.figure(figsize=(12, 8)) plt.plot(a_range, lyap, 'k.', markersize=0.5) plt.axhline(y=0, color='r', linestyle='--', linewidth=1) plt.xlabel('a', fontsize=20); plt.ylabel('λ', fontsize=20) plt.title('Lyapunov Exponent vs a', fontsize=16) plt.xlim([2, 4]) plt.tight_layout() plt.savefig('p5_lyapunov.png', dpi=300) plt.close()

Output

Figures