Assignment 4

Problem 1

Question

Let $G(x)=4x(1-x)$. Prove that for each positive integer $k$, there is an orbit of period $k$.

$G(x)=4x(1-x)$ maps $[0,1]$ onto itself. increasing on $[0,1/2]$, decreasing on $[1/2,1]$. two monotone laps.

perform lap count by induction $G^k$ has $2^k$ monotone laps. each lap of $G^{k-1}$ surjects $[0,1]\to [0,1]$, so its preimage under $G$ splits into two monotone pieces (one in each half). thus $G^k=G^{k-1}\circ G$ has $2\cdot 2^{k-1}=2^k$ laps.

fixed points; given that each lap maps some $[a,b]\subset [0,1]$ onto $[0,1]$. IVT says there’s at least one crossing of the diagonal. strict monotonicity gives exactly one. so $G^k$ has $2^k$ fixed points.

exact periods; $G^k$ has $2^k$ periodic points with period dividing $k$. subtract out lower divisors:

$$N(k)\ge 2^k-\sum _{d<k}{2}^d=2^k-(2^k-2)=2>0$$

since period-$k$ points come in orbits of size $k$, having $N(k)>0$ means at least one orbit.

Answer

$G^k$ has $2^k$ monotone laps, each giving a unique fixed point. Möbius inversion shows at least one period-$k$ orbit exists.

---

Problem 2

Question

For a general matrix $M=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$, what are the conditions on $a,b,c$ and $d$ which make the two-dimensional map $M\vec{v}(\mathrm{mod}1)$ continuous? Hint: prove the converse of Step 1, page 93.

torus ${\mathbb{T}}^2$ identifies points $(x,y)\sim (x+m,y+n)$ for integers $m,n$. map $S(\vec{v})=M\vec{v}(\mathrm{mod}1)$ is continuous iff well definned on equivalence class.

first step forward; if $a,b,c,d\in \mathbb{Z}$, then:

$$M\left(\begin{array}{c}x+m\\ y+n\end{array}\right)=M\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}am+bn\\ cm+dn\end{array}\right)$$

correction vector has integer entries, thus $M(x+m,y+n)\equiv M(x,y)(\mathrm{mod}1)$. seems well defined.

the converse is if $S$ is well-defined, then $(am+bn,cm+dn)\in {\mathbb{Z}}^2$ for all integers $m,n$.

plug $(m,n)=(1,0)$: get $(a,c)\in {\mathbb{Z}}^2$.

plug $(m,n)=(0,1)$: get $(b,d)\in {\mathbb{Z}}^2$.

Answer

continuous iff $a,b,c,d\in \mathbb{Z}$.

---

Problem 3

Question

Construct a periodic table (up to period 6) for the cat map. To do so, you will need to look at Steps 6, 7, and 9 on pages 95, 96 of the book.

cat map: $A=\left(\begin{array}{cc}2& 1\\ 1& 1\end{array}\right)$, $S(\vec{v})=A\vec{v}(\mathrm{mod}1)$.

Step 7; $A^n=\left(\begin{array}{cc}{F}_{2n}& F_{2n-1}\\ F_{2n-1}& F_{2n-2}\end{array}\right)$ where $F_0=F_1=1$, $F_n=F_{n-1}+F_{n-2}$.

Step 9; fixed points of $S^n$ count as $P(n)=|(F_{2n}-1)(F_{2n-2}-1)-F_{2n-1}^2|$.

fibonacci: $1,1,2,3,5,8,13,21,34,55,89,144,233,\dots$

computing $P(n)$:

$$\begin{array}{rl}P(1)& =|(2-1)(1-1)-1^2|=1\\ P(2)& =|(5-1)(2-1)-3^2|=5\\ P(3)& =|(13-1)(5-1)-8^2|=16\\ P(4)& =|(34-1)(13-1)-21^2|=45\\ P(5)& =|(89-1)(34-1)-55^2|=121\\ P(6)& =|(233-1)(89-1)-144^2|=320\end{array}$$

$P(n)$ counts all periodic points with period dividing $n$. subtract lower divisors to get exact period:

$$\begin{array}{rl}N(1)& =1\\ N(2)& =5-1=4\\ N(3)& =16-1=15\\ N(4)& =45-1-4=40\\ N(5)& =121-1=120\\ N(6)& =320-1-4-15=300\end{array}$$

orbits: divide by period.

period	$P(k)$	$N(k)$	orbits
1	1	1	1
2	5	4	2
3	16	15	5
4	45	40	10
5	121	120	24
6	320	300	50

---

Problem 4

Question

Consider the two-dimensional map given by $\vec{f}(x,y)=(2x+y,a-y^2)$

(a) Solve for all fixed points of $\vec{f}$. For what range of the parameter $a$ do (real) fixed points exist?

(b) Fix $a=0$ and for each of the fixed points from part (a), determine the stability (i.e. is it a sink, source, saddle, something else?)

(c) Find the critical value of $a$ above which the fixed points are of the same type.

A

fixed points: $\vec{f}(x,y)=(x,y)$ gives:

$$\{\begin{array}{l}2x+y=x\\ a-y^2=y\end{array}$$

first equation: $y=-x$.

second: $y^2+y-a=0$, so $y=\frac{-1\pm \sqrt{1+4a}}{2}$ with $x=-y$.

Answer

real fixed pts exist for $a\ge -\frac{1}{4}$.

B

at $a=0$: $y^2+y=0$ gives $(0,0)$ and $(1,-1)$.

jacobian:

$$J=\left(\begin{array}{cc}2& 1\\ 0& -2y\end{array}\right)$$

upper triangular → eigenvalues ${\lambda }_1=2$, ${\lambda }_2=-2y$.

at $(0,0)$: $\lambda =2,0$. magnitudes $2>1$ and $0<1$.

Answer

saddle.

at $(1,-1)$: $\lambda =2,2$. both $>1$.

Answer

source.

C

general fixed point has ${\lambda }_1=2$, ${\lambda }_2=-2y$. since $|{\lambda }_1|=2>1$ always, type depends on $|{\lambda }_2|$.

at $y_{-}=\frac{-1-\sqrt{1+4a}}{2}$: ${\lambda }_2=1+\sqrt{1+4a}>1$ for $a>-1/4$. always source.

at $y_{+}=\frac{-1+\sqrt{1+4a}}{2}$: ${\lambda }_2=1-\sqrt{1+4a}$.

$$|{\lambda }_2|<1⟺\sqrt{1+4a}<2⟺a<3/4$$

so $y_{+}$ is saddle for $a<3/4$, becomes source when $a>3/4$.

Answer

critical value: $a=\frac{3}{4}$. above this, both fixed points are sources.

---

Problem 5

Question

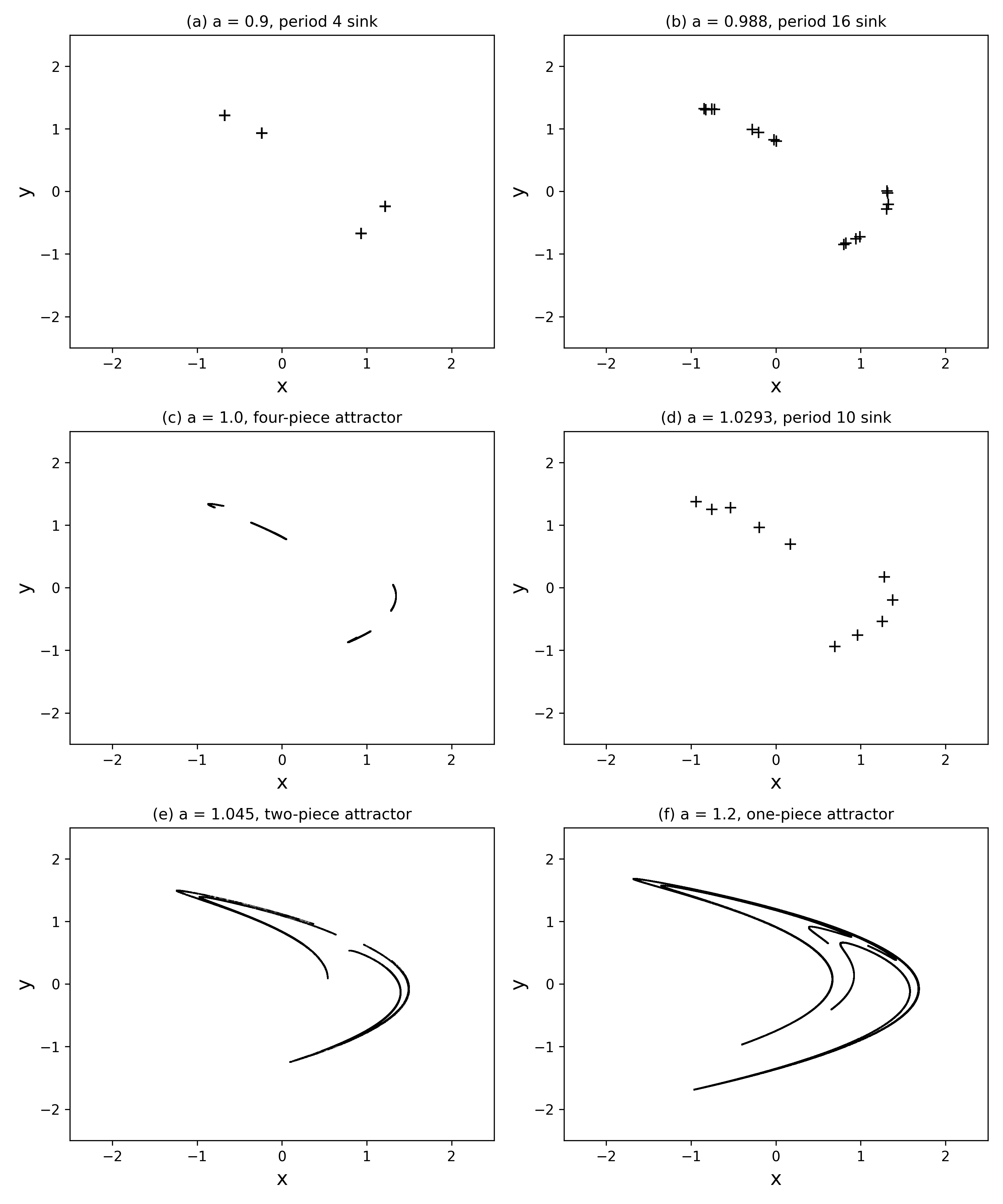
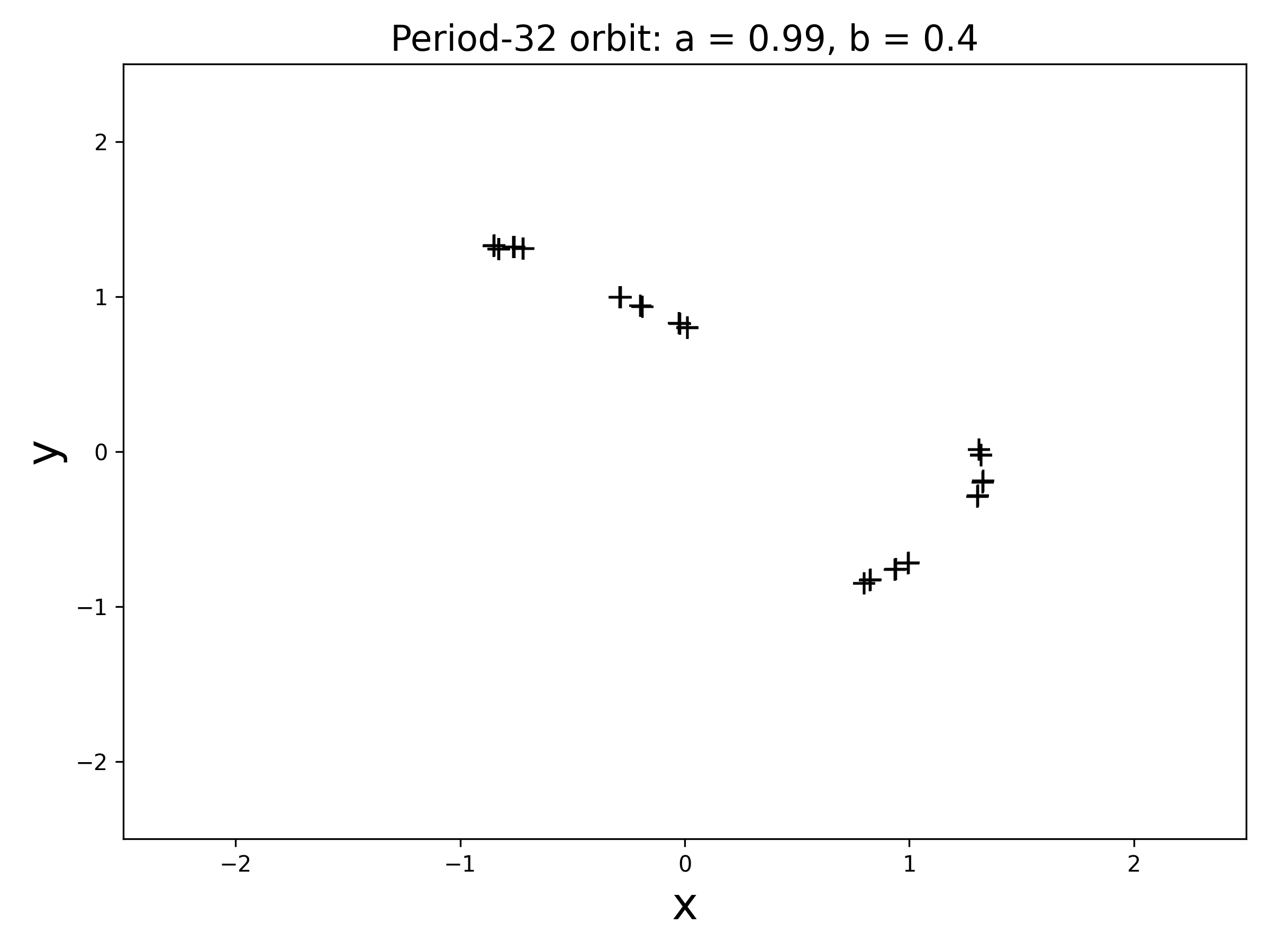
Use the code henon_iteration.m from the Files tab in the Matlab channel on Teams to recreate figure 2.17. In addition, find and plot a periodic orbit higher than period-16 (panel b). To do so, you’ll need to increase the number of iterates performed by the code, as well as the lag parameter specifying how many points are plotted.

Answer

rewrote MATLAB in python. henon map $x_{n+1}=a-x_n^2+b{y}_n$, $y_{n+1}=x_n$ with $b=0.4$.

fig 2.17 recreation chaotic panels used $10^5$ iterates to fill out the attractor shape.

found period 32 at $a=0.99$. the 32 points cluster in pairs around the 16 locations from the previous bifurcation. ran $10^5$ iterates, plotted last 160.

Code

Python

import numpy as np import matplotlib.pyplot as plt def henon(a, b, x0, y0, N): x, y = np.zeros(N + 1), np.zeros(N + 1) x[0], y[0] = x0, y0 for i in range(N): x[i + 1] = a - x[i]**2 + b * y[i] y[i + 1] = x[i] return x, y def detect_period(x, max_period=256, tol=1e-6): for p in range(1, max_period + 1): n_check = min(2 * p, 200) matches = sum(abs(x[-1 - i] - x[-1 - i - p]) < tol for i in range(n_check)) if matches / n_check > 0.95: return p return -1 b = 0.4 x0, y0 = 0.0, 0.0 # 2.17 panels = [ (0.9, "period 4 sink"), (0.988, "period 16 sink"), (1.0, "four piece attractor"), (1.0293, "period 10 sink"), (1.045, "two-piece attractor"), (1.2, "one-piece attractor"), ] fig, axes = plt.subplots(3, 2, figsize=(10, 12)) for idx, (a, desc) in enumerate(panels): row, col = divmod(idx, 2) ax = axes[row][col] if a in (1.0, 1.045, 1.2): x_h, y_h = henon(a, b, x0, y0, 10**5) ax.plot(x_h[50000:], y_h[50000:], 'k.', markersize=0.3) else: x_h, y_h = henon(a, b, x0, y0, 10**4) p = detect_period(x_h) ax.plot(x_h[-max(5*p, 50):], y_h[-max(5*p, 50):], 'k+', markersize=8) ax.set(xlim=(-2.5, 2.5), ylim=(-2.5, 2.5), xlabel='x', ylabel='y') ax.set_title(f'({"abcdef"[idx]}) a = {a}, {desc}', fontsize=11) plt.tight_layout() plt.savefig('2_17.png', dpi=300) plt.close() # period 32 graph x3, y3 = henon(0.99, b, x0, y0, 10**5) p3 = detect_period(x3, max_period=128) plt.figure(figsize=(8, 6)) plt.plot(x3[-5*p3:], y3[-5*p3:], 'k+', markersize=10) plt.xlabel('x', fontsize=20); plt.ylabel('y', fontsize=20) plt.title(f'Period-{p3} orbit: a = 0.99, b = 0.4', fontsize=16) plt.xlim(-2.5, 2.5); plt.ylim(-2.5, 2.5) plt.tight_layout() plt.savefig('period32.png', dpi=300) plt.close()

Output

Figures