Assignment 1

Question 1

Let p be a fixed point of a nonlinear map $f$ . Given an $ϵ>0$, find a geometric condition on $f$ under which all points $x$ in $N_{ϵ}(p)$ are in the basin of $p$. Use cobweb plot analysis to explain your reasoning. Hint: By geometric condition, I mean some constraint on $f$ and/or $f^{\prime }$ in the neighborhood of $p$. One example condition that you can improve upon:

$$\forall x\in (p-ϵ,p),f(x)>x\&f(x)<p$$ $$\forall x\in (p,p+ϵ),f(x)<x\&f(x)>p$$

In more words and less notation: provided $f(x)$ remains between the lines $y=x$ and $y=p$ in the epsilon neighborhood of $p$, all points in the neighborhood are in the basin of $p$. This question is deeper than you may think at first, and showing your condition works for a single example is not proving that it works for all example functions f . Your condition needs to work for all f .

Answer

Geometric Condition

We can use the local stability criterion as our geometric condition:

$$|f^{\prime }(p)|<1$$

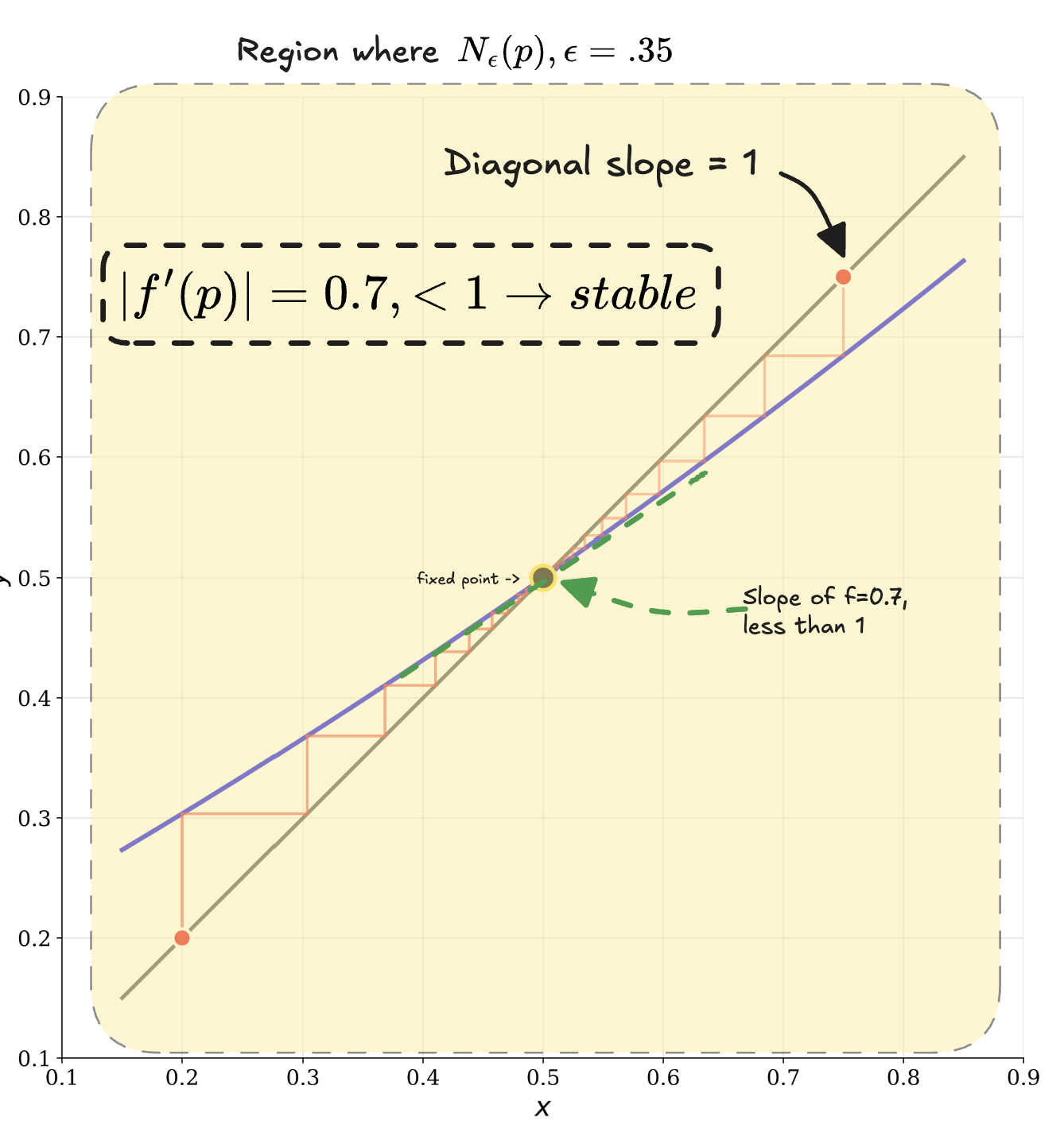
Cobweb Plot

In the plot below, we start from two different pointsi within the $N_{ϵ}(p)$ region. Iterations lead inward toward the sink, and since curve $f(x)$ (in blue) crossed $y=x$ with a shallow slope less than 1, we can ensure that the iterations will converge.

Proof

We now prove this condition guarantees convergence for all functions $f$.

Pick some value of $\lambda$ $s.t.$:

$$|f^{\prime }(p)|<\lambda <1$$

Thus by the continuity of $f^{\prime }$, $\exists$ some $ϵ>0$ $s.t.$ $\forall$ $x$ in the neighborhood $N_{ϵ}(p)$, we have:

$$|f^{\prime }(x)|<\lambda \forall x\in N_{ϵ}(p)$$

We can then apply the Mean Value Theorem, such that for any $x$ in the neighborhood of $N_{ϵ}(p)$, $\exists$ $c$ between $x$ and $p$ such that:

$$f(x)-f(p)=f^{\prime }(c)(x-p)$$

And, since $f(p)=p$ by definition of a fixed point, and geometric conditions states that $|f^{\prime }(c)|<\lambda$, we get:

$$|f(x)-p|=|f^{\prime }(c)|\cdot |x-p|<\lambda |x-p|$$

We then repeat the contraction for all $f^n$ ( could be done with something like the Banach Fixed Point Theorem ), such that each time we reapply $f$,the distance from $p$ will shrink by at least $\lambda$:

$$\begin{array}{rl}|f(x)-p|& <\lambda |x-p|\\ |f^2(x)-p|& <\lambda |f(x)-p|<{\lambda }^2|x-p|\\ & ⋮\\ |f^n(x)-p|& <{\lambda }^n|x-p|\end{array}$$

Thus, because $\lambda <1$, we see ${\lim }_{n\to \infty }{\lambda }^n=0$, therefore:

Result

$$\underset{n\to \infty }{\lim }{f}^n(x)=p$$

---

Question 2

The map $f(x)=2x^2-5x$ on $\mathbb{R}$ has fixed points at $x=0$ and $x=3$.

• Find a period two orbit for f by solving f 2(x) = x for x.
• What is the stability of the orbit?

Hint: For this problem and the next, you will need to factor a degree 4 polynomial. This can be done by hand without any horrific formulas if you think about what you already know about the roots. 1

Answer

Finding Period Two Orbits for $f^2(x)$

Compose:

$$\begin{array}{rl}f(f(x))& =2(2x^2-5x{)}^2-5(2x^2-5x)\\ & =2(4x^4-20x^3+25x^2)-10x^2+25x\\ & =8x^4-40x^3+50x^2-10x^2+25x\\ & =8x^4-40x^3+40x^2+25x\end{array}$$

Then plug into $f^2(x)=x$:

$$\begin{array}{rl}8x^4-40x^3+40x^2+25x& =x\\ 8x^4-40x^3+40x^2+24x& =0\end{array}$$

Factor polynomial

$$8x(x^3-5x^2+5x+3)=0$$

And given that we know the fixed points are $x=0$ and $x=3$, and $x$ has been factored out, we can divide by $(x-3)$ to find the rest of the roots.

$$\frac{(x^3-5x^2+5x+3)}{(x-3)}=x^2-2x-1$$

Plugging into quadratic formula:

$$x=\frac{-(-2)\pm \sqrt{(-2{)}^2-4(1)(-1)}}{2(1)}=\frac{2\pm \sqrt{8}}{2}=1\pm \sqrt{2}$$

Yielding:

Answer

$$\{1-\sqrt{2},1+\sqrt{2}\}$$

Finding Stabllty

To find stability, we have to find derivatives of $f(x)$ and $f^2(x)$:

Derivative of $f(x)$:

$$f^{\prime }(x)=4x-5$$

Plug in two orbit points:

$$\begin{array}{rl}{f}^{\prime }(p)& =4(1-\sqrt{2})-5=-1-4\sqrt{2}\\ f^{\prime }(q)& =4(1+\sqrt{2})-5=-1+4\sqrt{2}\end{array}$$

Calculate the $\lambda$ value

$$\begin{array}{rl}\lambda & =(-1-4\sqrt{2})(-1+4\sqrt{2})\\ & =(-1{)}^2-(4\sqrt{2}{)}^2\\ & =1-16(2)\\ & =1-32\\ & =-31\end{array}$$

Answer

Orbit is unstable as $|\lambda |=31>1$

---

Problem 3

Let $G(x)=4x(1-x)$

• Find the fixed points and period two points of $G$ and demonstrate that they are sources using $G\prime$ and/or $(G2)\prime$.
• Continue the periodic table for $G$ begun in Table 1.3. In particular how many periodic orbits of (minimum) period k does G have, for each k ≤ 10?

Hint: The pattern is not simple. Your table should look something like this:

Period $k$	Number of fixed points of $G^k$	Proper divisors of $k$	Number of fixed points due to periods $<k$	Number of fixed points due to peiod $k$ only	Orbits of period $k$
1	2	1	0	2	2
2	4	1	2	2	1
3	8	1	2	6	2
4	16	1,2	4	12	3
5
6
7
8
9
10

Answer

Fixed Points and Period Two Points

We can find the fixed points with $G(x)=x$:

$$4x(1-x)=x⟹4x-4x^2=x⟹x(3-4x)=0$$

Thus fixed points are $x=0$ and $x=\frac{3}{4}$.

Finding stability with derivative:

$$G^{\prime }(x)=4-8x$$

For $x=0$, $G^{\prime }(0)=4$, $|4|>1$ and is thus a source.

For $x=\frac{3}{4}$, $G^{\prime }(\frac{3}{4})=4-8(\frac{3}{4})=-2$, $|-2|>1$ and is thus a source.

To find the period 2 orbit, we plug into $G^2(x)=x$:

$$-64x^4+128x^3-80x^2+15x=0$$

and factor:

$$x(-64x^3+128x^2-80x+15)=0$$

and since $x=\frac{3}{4}$ is also a root:

$$64x^3-128x^2+80x-15=(4x-3)(16x^2-20x+5)$$

We can now use them to construct the period two orbit via quadratic $16x^2-20x+5=0$:

$$x=\frac{20\pm \sqrt{80}}{32}=\frac{5\pm \sqrt{5}}{8}$$

And then we can find the stablity with derivatives:

$$\begin{array}{rl}\lambda & =G^{\prime }(p_1)\cdot G^{\prime }(p_2)\\ & =\left(-1+\sqrt{5}\right)\left(-1-\sqrt{5}\right)\\ & =1-5\\ & =-4\end{array}$$

Answer

$$|\lambda |=4>1$$

thus period two orbit is a source.

Table Completion

Here is the completed table:

Period $k$	Number of fixed points of $G^k$	Proper divisors of $k$	Number of fixed points due to periods $<k$	Number of fixed points due to peiod $k$ only	Orbits of period $k$
1	2	1	0	2	2
2	4	1	2	2	1
3	8	1	2	6	2
4	16	1,2	4	12	3
5	32	1	2	30	6
6	64	1,2,3	10	54	9
7	128	1	2	126	18
8	256	1,2,4	16	240	30
9	512	1,3	8	504	56
10	1024	1,2,5	34	990	99

---

Question 4

Let $l(x)=ax+b$, where $a$ and $b$ are constants. For which values of $a$ and $b$ does $l$ have

• an attracting fixed point?
• a repelling fixed point?
• a neutral point?

Answer

Before any sub questions, lets solve for fixed points $l(x)=x$

$$\begin{array}{rl}ax+b& =x\\ ax-x& =-b\\ x(a-1)& =-b\\ x^k& =\frac{-b}{a-1}(a\ne 1)\end{array}$$

Derivative must also be a constant from the linearity of $l(x)$:

$$l^{\prime }(x)=a$$

THe only thing affecting stability here will be $|a|$, regardless of $b$ or fixed point.

Attracting Fixed Point

By definition an attracting fixed point must satisfy $|l^{\prime }(x^k)|<1$

Therefore:

Answer

$$|a|<1anda\ne 1$$

Repelling Fixed Point

By definition a repelling fixed point must satisfy $|l^{\prime }(x^k)|>1$

Therefore:

Answer

$$|a|>1$$

and also $b$ can be any real value.

Neutral Fixed Point

By definition a neutral fixed point must satisfy $|l^{\prime }(x^k)|=1$

Answer

$$|a|=1⟹a=1ora=-1$$

And when $a=-1$, $\exists$ a fixed point at $x^k=\frac{-b}{-2}$ for any real $b$

For when $a=1$, if $b=0$, every point fixed, else no fixed points exist.

---

Question 5

Let $x_1<\cdots <x_8$ be the eight fixed points of $G^3(x)$ where $G(x)=4x(1-x)$. Clearly $x_1=0$.

• For which $i$ is $x_i=\frac{3}{4}$?
• Group the remaining six points into two orbits of three points each.

Hint: It may help to consult Figure 1.10(c). The most elegant solution uses the chain rule. You need not compute the actual values of the xi

Answer

Finding Index of $i$ where Midpoint is 3/4

Not sure if this is “cheating” or not, but Figure 1.10C does seem to just show the ordering of fixed points for $G^3(x)$.

Visually, it seems as though there are 5 fixed points less than 3/4, and thus:

Answer

$$i=6$$

Grouping Remaining Points into Orbits

The other 6 points form two period 3 orbits. Lets define them:

Orbit 1:

$$\{p_{1,1},p_{1,2},p_{1,3}\}$$

Orbit 2:

$$\{p_{2,1},p_{2,2},p_{2,3}\}$$

Chain rule yields that any point $p$ in one of these period 3 orbits ($p_1,p_2,p_3$) where $G(p_1)=p_2$, $G(p_2)=p_3$, $G(p_3)=p_1$, …, we get:

$$(G^3{)}^{\prime }(p_i)=G^{\prime }(p_1)\cdot G^{\prime }(p_2)\cdot G^{\prime }(p_3)$$

It is the same product for all 3 points independent of order.

We can compute $(G^3{)}^{\prime }(x)$ with each to see if they yield the same value, but we can sort of infer this from the figure, just that points alternate in their sign but vary in magnitude. Points belonging to the same orbit will have the same derivative value for $(G^3{)}^{\prime }(x)$.

Thus:

Answer

Orbit 1: $\{x_2,x_4,x_7\}$

Orbit 2: $\{x_3,x_5,x_8\}$

We can very by computing at each point, but it is not exactly necessary.

---

Source Code

Problem 1

Python

import numpy as np import matplotlib.pyplot as plt plt.rcParams['figure.figsize'] = (10, 10) plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'serif' plt.rcParams['lines.linewidth'] = 2.5 fig, ax = plt.subplots(figsize=(10, 10)) # function we analyzin def f(x): p = 0.5 return p + 0.7 * (x - p) + 0.15 * (x - p)**2 p = 0.5 epsilon = 0.35 xlim = (p - epsilon, p + epsilon) x_plot = np.linspace(xlim[0], xlim[1], 1000) y_plot = f(x_plot) ax.plot(x_plot, y_plot, 'b-', linewidth=3, zorder=3) ax.plot(x_plot, x_plot, 'k-', linewidth=2.5, alpha=0.7, zorder=2) x0_left = 0.2 x0_right = 0.75 # cobweb iteration for x0, alpha_val in [(x0_left, 0.7), (x0_right, 0.5)]: x = x0 for i in range(20): y = f(x) ax.plot([x, x], [x, y], 'r-', alpha=alpha_val, linewidth=1.8, zorder=4) ax.plot([x, y], [y, y], 'r-', alpha=alpha_val, linewidth=1.8, zorder=4) x = y ax.plot(p, p, 'ko', markersize=16, zorder=6, markeredgewidth=2.5, markeredgecolor='gold') # start pointgs ax.plot(x0_left, x0_left, 'ro', markersize=12, zorder=5, markeredgewidth=2, markeredgecolor='white') ax.plot(x0_right, x0_right, 'ro', markersize=12, zorder=5, markeredgewidth=2, markeredgecolor='white') # plot format ax.set_xlim(xlim[0] - 0.05, xlim[1] + 0.05) ax.set_ylim(xlim[0] - 0.05, xlim[1] + 0.05) ax.set_xlabel('$x$', fontsize=18) ax.set_ylabel('$y$', fontsize=18) ax.set_aspect('equal') ax.grid(True, alpha=0.3, linewidth=1) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) plt.tight_layout() plt.show()

Output