Conjugacy and the Logistic Map

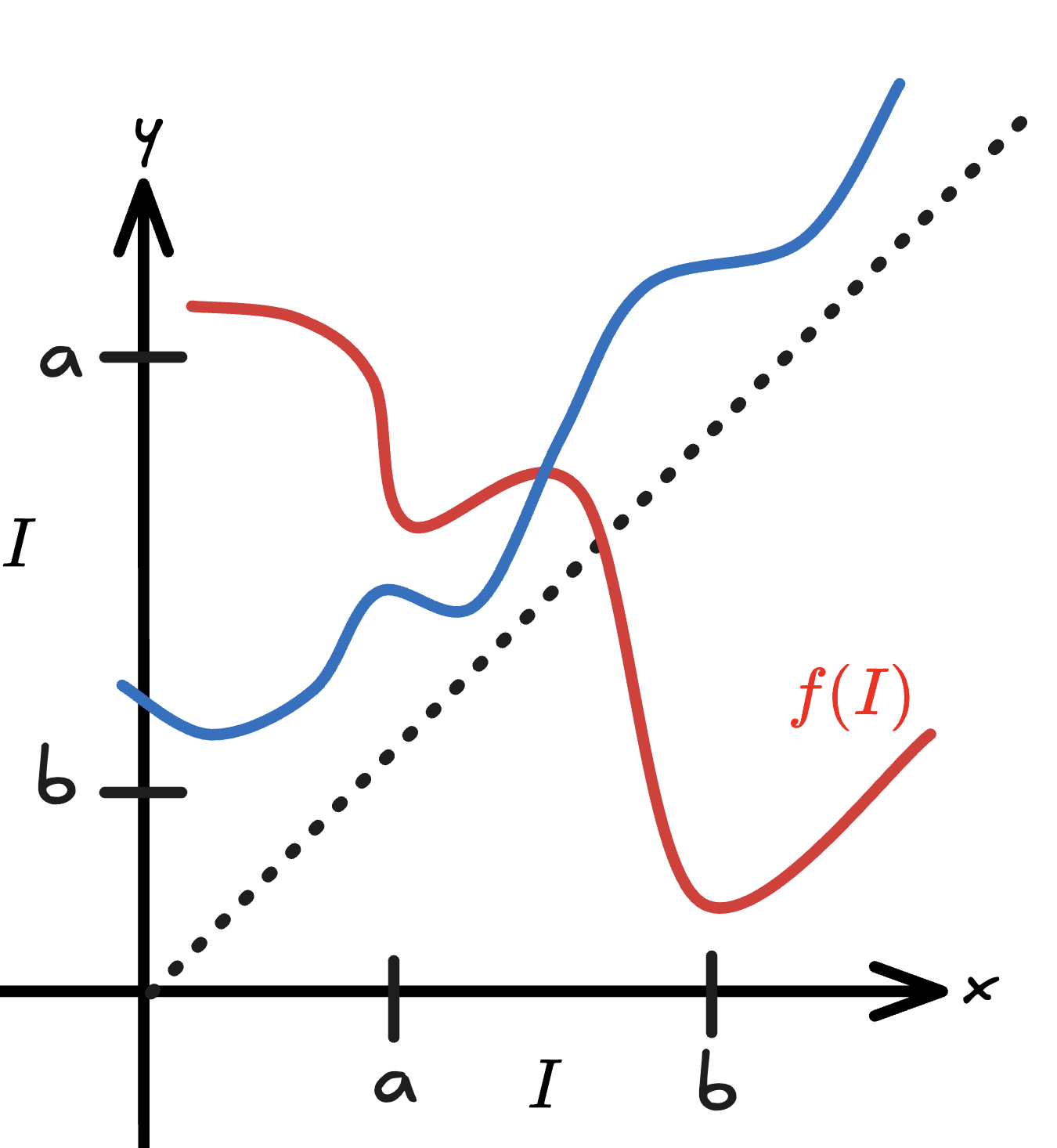
If we want to show that $G(x)=4x(1-x)$ has chaotic orbits, we will do it by comparing with $T(x)$ ( our Tent Map ).

For each point in the Tent Map domain $\{0,1\}$, there is a companion point $C(x)$ in the domain of $G$ that imitates its dynamics.

We say the maps $f$ and $g$ are conjugate if they are related by a continuous one to one change of coordinates.

$"\\usepackage{tikz-cd}\n\\begin{document}\n\\begin{tikzcd}[row sep=3em, column sep=4em]\n {[0,1]} \\arrow[r, \"T\"] \\arrow[d, \"C\"'] & {[0,1]} \\arrow[d, \"C\"] \\\\\n {[0,1]} \\arrow[r, \"G\"'] & {[0,1]}\n\\end{tikzcd}\n\\end{document}"$

source code

Example

$$C\circ f=g\circ C$$

or

$$\begin{array}{rl}\underset{\text{annialates}}{\underbrace{C^{-1}\circ C}}\circ f& =C^{-1}\circ g\circ C\\ f& =C^{-1}\circ g\circ C\end{array}$$

The maps $G$ and $T$ are conjugate by:

$$C(x)=\frac{(1-\cos (\pi x))}{2}\text{1 to 1, continuous}$$

and:

$$C(T(x))=G(C(x))$$

For $0\le x\le \frac{1}{2}$:

$$\begin{array}{rl}G(C(x))& =4C(x)(1-C(x))\\ & =4\left(\frac{1-\cos \pi x}{2}\right)\left(\frac{1+\cos \pi x}{2}\right)\\ & =(1-{\cos }^2\pi x)\\ & ={\sin }^2\pi x\end{array}$$ $$\underset{\text{trig double }\angle \text{ identity!}}{\underbrace{\begin{array}{rl}C(T(x))& =\frac{1-\cos (2\pi x)}{2}\\ & ={\sin }^2\pi x\end{array}}}$$

Idea

Two ways of getting from domain of $G$ to range of $G$ after $n$ iterations:

1. Evaluate $G^n(x)$ directly — expensive, analytically intractable for large $n$

2. Use conjugacy: since $C\circ T=G\circ C$, induction gives $C\circ T^n=G^n\circ C$, so:

   $$G^n(x)=C\left(T^n\left(C^{-1}(x)\right)\right)$$

   Map $x$ into T’s domain via $C^{-1}$, iterate the simpler tent map $n$ times, then map back. Orbit structure of $G$ is exactly that of $T$, just seen through the lens $C$.

Suppose $T(x)=x$ for a Fixed Point and $C^{\prime }(x)\ne 0$ $\left(x=\frac{2}{3}\right)$ then:

$$\begin{array}{rl}{C}^{\prime }(x)\cdot T^{\prime }(x)& =G^{\prime }(C(x))C^{\prime }(x)\\ \Rightarrow T^{\prime }(x)& =G^{\prime }(C(x))\end{array}$$

So stability of Fixed Point of $T$ and stability of Fixed Point $C(x)=\frac{3}{4}$, for $G$ are the same

---

Transition Graphs

Theorem (Covering implies fixed point)

Let $f$ be a continuous map of $\mathbb{R}$ and let $I=\{a,b\}$ be an interval such that:

$$f(I)\supseteq I$$

Then $f$ has a Fixed Point in $I$.

The blue line in the figure is the counterexample — a function where $f(I)⊉I$, so IVT doesn’t force a fixed point.

In topology, the general version is Brouwers Fixed Point Theorem.

---

Setup

A partition of the interval is a collection of subintervals that are pairwise disjoint (except at endpoints) whose union is the whole interval.

For both $G$ and $T$, the natural partition is $\{L,R\}$:

$$L=\left[0,\frac{1}{2}\right],R=\left[\frac{1}{2},1\right]$$

Definition: Draw an arrow $A\to B$ in the transition graph if and only if $f(A)\supseteq B$ — ”$f$ of $A$ covers $B$“.

The covering condition matters because: if $f(A)\supseteq B$, then by the Intermediate Value Theorem there exists a point in $A$ that maps into $B$. Covering arrows are existence guarantees for orbits.

---

Computing the Graph for $T$

The Tent Map $T$ with $\mu =2$:

• $T(L)=T\left(\left[0,\frac{1}{2}\right]\right)=[0,1]\supseteq L$ and $\supseteq R\Rightarrow L\to L,L\to R$
• $T(R)=T\left(\left[\frac{1}{2},1\right]\right)=[0,1]\supseteq L$ and $\supseteq R\Rightarrow R\to L,R\to R$

All four arrows exist. The Tent Map transition graph is completely connected.

$"\\usepackage{tikz}\n\\usetikzlibrary{positioning, arrows.meta}\n\\begin{document}\n\\begin{tikzpicture}[\n box/.style={draw, circle, minimum size=1.2cm, font=\\large, thick},\n ->, >=Stealth, semithick, bend angle=25\n]\n \\node[box] (L) {$L$};\n \\node[box, right=3cm of L] (R) {$R$};\n \\draw (L) edge[loop above, looseness=6] (L);\n \\draw (L) edge[bend left] (R);\n \\draw (R) edge[bend left] (L);\n \\draw (R) edge[loop above, looseness=6] (R);\n\\end{tikzpicture}\n\\end{document}"$

source code

By conjugacy, $G=4x(1-x)$ has the same graph — $G$ also maps both $L$ and $R$ surjectively onto $[0,1]$.

---

A path of length $n$ in the graph is a sequence $A_0\to A_1\to \cdots \to A_n$ where each arrow is a valid transition. This corresponds to an admissible itinerary; there genuinely exists a point $x\in A_0$ whose orbit visits $A_1,A_2,\dots ,A_n$ in order.

Consequence of complete connectivity: Every infinite sequence over $\{L,R\}$ is admissible. That’s an uncountable family of distinct symbolic trajectories, each encoding a genuinely different orbit.

Periodic orbits from cycles: A cycle of length $k$ in the graph (e.g. $L\to R\to L\to R\to \cdots$ returning to $L$) guarantees a period-$k$ orbit exists in that sequence of intervals. Since all arrows exist, cycles of every length exist → infinitely many periodic orbits.

---