Discusses the concept of discrete random variables and their probability distributions.
What is a Discrete Random Variable?
Discrete outcomes are those that can be counted and are distinct from one another. A discrete random variable is a variable that can take on a finite number of values. For example, the number of heads in a series of coin flips is a discrete random variable.
This differs from continuous random variables, which can take on any value within a range. For example, the height of a person is a continuous random variable.
We can model a discrete random variables outcomes through a binomial distribution, which describes the probability of getting a certain number of successes in a fixed number of trials.
import matplotlib.pyplot as plt
import numpy as np
# Create figure with two subplots side by side
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Discrete example: Coin flips
outcomes = [0, 1, 2, 3, 4]
probabilities = [0.0625, 0.25, 0.375, 0.25, 0.0625] # Binomial probabilities for 4 flips
ax1.bar(outcomes, probabilities, width=0.5)
ax1.set_title('Discrete: Number of Heads in 4 Coin Flips')
ax1.set_xlabel('Number of Heads')
ax1.set_ylabel('Probability')
# Continuous example: Height distribution
x = np.linspace(150, 190, 100)
y = np.exp(-((x - 170)**2)/(2*100)) / (np.sqrt(2*np.pi*100)) # Normal distribution
ax2.plot(x, y)
ax2.fill_between(x, y, alpha=0.3)
ax2.set_title('Continuous: Height Distribution')
ax2.set_xlabel('Height (cm)')
ax2.set_ylabel('Probability Density')
plt.tight_layout()
plt.show()Continuous Random Variables
Continuous Random Variables are those that can take on any value within a range. For example, the height of a person is a continuous random variable.
To contrast, a continuous random variable has a infinitely dividable range of values, with “infinite precision”
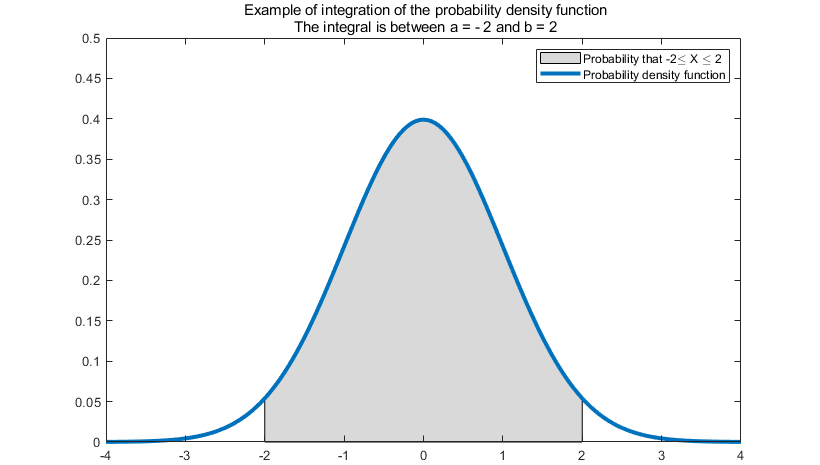
There is a lot more to cover on what we can do with these random variables, but I already have several notes written for another class, namely CH2 - Random Variables.