Depth First Search

Depth-First Search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at a designated start node (or an arbitrary node in a general graph) and explores as far as possible along each branch before backtracking.

Properties

• DFS produces a DFS forest on $V$ via the predecessor relation; in an undirected graph, each tree corresponds to a connected component.
• Each vertex $v$ receives discovery time $d[v]$ and finish time $f[v]$; the intervals $[d[u],f[u]]$ satisfy the parenthesis property (either disjoint or one properly contains the other).
• Edge classification in directed graphs: tree, back, forward, cross; in undirected graphs, every non-tree edge is a back edge.
• In a DAG, ordering vertices by decreasing finish time yields a valid topological order.

Pseudocode

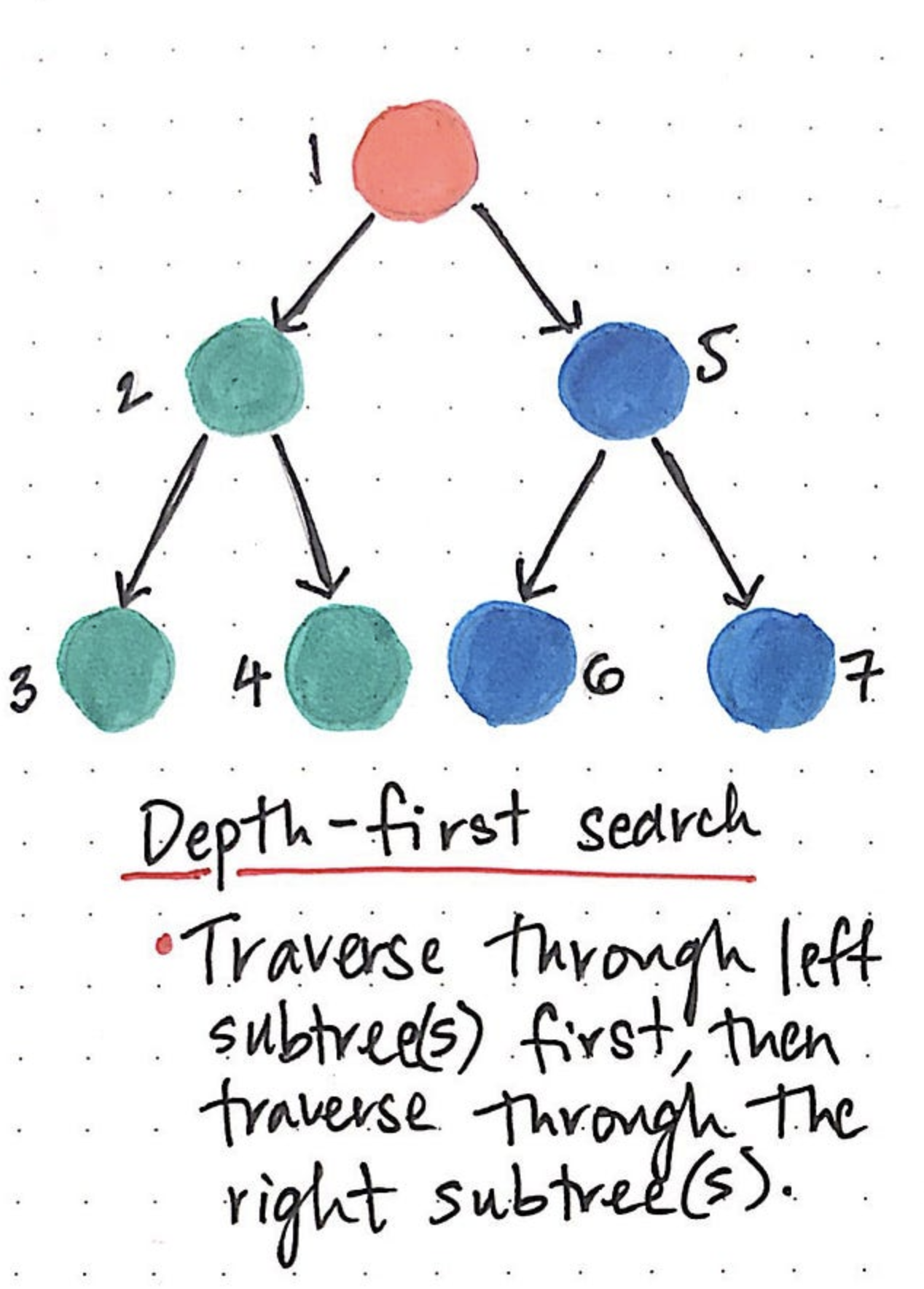
Formal Definition

Let $G=(V,E)$ be a finite directed or undirected graph and optionally a designated start vertex $s\in V$. Depth-First Search (DFS) explores edges out of the most recently discovered vertex that still has unexplored incident edges.

$$\begin{array}{rl}\text{State:}& c:V\to \{\text{white},\text{gray},\text{black}\},\pi :V\to V\cup \{\mathrm{NIL}\},\\ & d:V\to \mathbb{N},f:V\to \mathbb{N},t\in \mathbb{N}.\end{array}$$

Initialization:

$$\forall v\in V:c[v]\leftarrow \text{white},\pi [v]\leftarrow \mathrm{NIL};t\leftarrow 0.$$

Procedure:

$$\begin{array}{rl}\text{DFS}(G,s):& \text{if }s\text{ is given then }\text{DFS\_Visit}(s).\\ & \text{for each }v\in V\text{ with }c[v]=\text{white}:\text{DFS\_Visit}(v).\end{array}$$

Recursive step:

$$\begin{array}{rl}\text{DFS\_Visit}(u):& c[u]\leftarrow \text{gray};d[u]\leftarrow t\leftarrow t+1;\\ & \text{for each edge }(u,v)\in E\text{ in any fixed order:}\\ & \text{if }c[v]=\text{white}\text{ then }\pi [v]\leftarrow u;\text{DFS\_Visit}(v);\\ & c[u]\leftarrow \text{black};f[u]\leftarrow t\leftarrow t+1.\end{array}$$

Outputs:

$$\begin{array}{rl}& \pi \text{ induces a DFS forest }\mathcal{F}\text{ over }V;\\ & d[v]\text{ and }f[v]\text{ are the discovery and finish times of }v.\end{array}$$

Edge classification (directed graphs):

$$\begin{array}{rl}& \text{Tree edge: }(u,v)\text{ where }c[v]=\text{white}\text{ when first explored}.\\ & \text{Back edge: }d[v]<d[u]<f[u]<f[v].\\ & \text{Forward edge: }d[u]<d[v]<f[v]<f[u].\\ & \text{Cross edge: }d[v]<f[v]<d[u]<f[u]\text{ or vice versa}.\end{array}$$

Parenthesis property:

$$\forall u\ne v:[d[u],f[u]]\text{ and }[d[v],f[v]]\text{ are either disjoint or one properly contains the other.}$$

Reachability (with start $s$):

$$v\text{ is reachable from }s⟺v\text{ lies in the DFS tree rooted at }s\text{ in }\mathcal{F}.$$

Time and space:

$$T(G)=\Theta (|V|+|E|),S(G)=\Theta (|V|).$$