Algo hw 12

Self Reducibility

Show how the optimization version of vertex cover problem is polynomial time-reducible to its decision version. The optimization version, known as min vertex cover problem, is “given a graph $G$ , find the minimum set of vertices that cover all the edges in $G$ ”. The decision version is “given a graph $G$ and a constant $k$ , is there a vertex cover of at most $k$ vertices?” Here, we say a vertex “covers” an edge if and only if the vertex is an end- node of the edge.

Reduction to Decision Version

We start with the two phases, finding the minimum size using inbary search, and constructing an actual minimum vertex using the vertex elimination.

Using the given graph $G = (V, E)$ with value of $n = ∣ V ∣$ vertices, we use binary search with the following decision oracle:

Initialize: ℓ = 0,; r = n While ℓ < r : m = ⌊(ℓ + r) /2 ⌋ if DEC-VC (G, m) = YES : r = m else : ℓ = m + 1 Return k^{*} = ℓ

This yields a big $O$ complexity of $O (lo g n)$ calls to $D E V - V C$ , where each takes polynomial time.

Now that we know the value of $k^{*}$ , we can construct an actual minimum vertex cover $C$ :

C = \emptyset k = k^{*} V^{'} = V (remaining vertices) For each vertex v \in V : G^{'} = G [V^{'} ∖ v] (induced subgraph without v) if DEC-VC (G^{'}, k - 1) = NO : C = C \cup v k = k - 1 V^{'} = V^{'} ∖ v Return C

We notice that when DEC-VC( $G^{'}, k - 1$ ) returns NO, then vertex $v$ MUST be in every vertex cover of the size $k$ for current graph.

Now we have the information necessary for a proof via contradiction:

We suppose that $v$ is not needed. If this is the case, then there exists a vertex cover of size $k$ not containing $v$ , where this dover only uses vertices from $V^{'} ∖ {v}$ . Therefore, $G^{'}$ has a vertex cover of size $\leq k - 1$ , which is a contradiction.

This algorithm terminates with $∣ C ∣ = k^{*}$ because we only add a vertex to $C$ when its essential, we decrement $k$ each time we add a vertex, and we started with exactly $k^{*}$ slots to fill.

This yields the final complexity:

Phase 1: O (lo g n) oracle calls Phase 2: O (n) oracle calls (one per vertex) Total: O (n + lo g n) = O (n) oracle calls

Given that each phase call is completed in polynomial time, that means the full reduction also runs in polynomial time. $■$

Set Packing and Independent Set

Prove that $SET - P A C K I NG \leq_{p} I N D EPEN D ENT - SET$ , that is, the $SET - P A C K I NG$ decision problem is polynomial-time reducible to the $I N D EPEN D ENT - SET$ decision problem. Feel free to use an illustration if it helps. The definitions of these two decision problems are summarized below.

$SET - P A C K I NG$ : Given a set $U$ of elements, a set of subsets $S_{1}, S_{2}, ..., S_{m}$ of $U$ , and an integer $k$ , does there exist a set of at least $k$ subsets that are pairwise disjoint (i.e., intersection = $\emptyset$ between every pair)?
$I N D EPEN D ENT - SET$ : Given a graph $G = (V, E)$ and an integer $k$ , is there a subset of vertices $S \subseteq V$ such that $∣ S ∣ \geq k$ and, for each edge in $E$ , at most one — but not both — of its end nodes is in S?

(Note we’ve already proved in class that INDEPENDENT-SET $\leq_{p}$ SET-PACKING, so this proof leads to it that INDEPENDENT-SET $\equiv_{p}$ SET-PACKING, that is, these two problems are equally hard computationally.)

Make sure to give a complete proof based on the Karp reduction definition (which is for decision problems) by including the two parts---(1) the polynomial-time construction algorithm and (2) the equivalence of solutions to the two problems.

Constructing the Reduction

Given a SET-PACKING instance $(U, {S_{1}, S_{2}, \dots, S_{m}, k})$ , construct an INDEPENDENT-SET instance $(G, k)$ as follows:

Graph G = (V, E) where: V = v_{1}, v_{2}, ..., v_{m} (one vertex per subset) E = (v_{i}, v_{j}) : S_{i} \cap S_{j} \neq = \emptyset,; i \neq = j (edge iff subsets intersect)

Keeping the same value of $k$ . In essense, the two subsets are disjoint, their corresponding vertices are not connected by an edge.

A demo would look something like:

U S_{1} S_{2} S_{3} S_{4} S_{5} k = 2 = {1, 2, 3, 4, 5} = {1, 2} = {2, 3} = {3, 4} = {4, 5} = {1, 5}

Their intersections would look like:

S_{1} \cap S_{2} S_{2} \cap S_{3} S_{3} \cap S_{4} S_{4} \cap S_{5} S_{1} \cap S_{5} = {2} \neq = \emptyset \to e d g e (v_{1}, v_{2}) = {3} \neq = \emptyset \to e d g e (v_{2}, v_{3}) = {4} \neq = \emptyset \to e d g e (v_{3}, v_{4}) = {5} \neq = \emptyset \to e d g e (v_{4}, v_{5}) = {1} \neq = \emptyset \to e d g e (v_{1}, v_{5})

All other pairs are disjoint. See Figure 1 for a rough visualization of this graph.

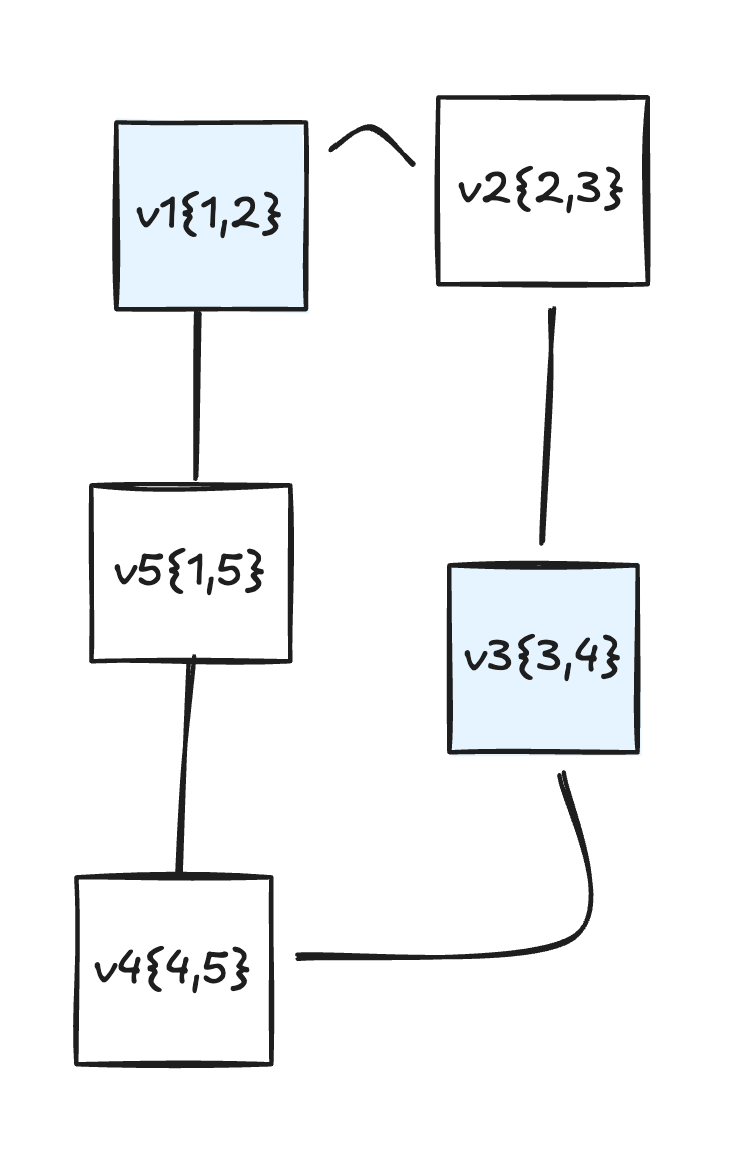
Resultant Graph(rough)

To proove the correctness, we must now define our theorem that SET-PACKING has a solution of size $\geq k ⟺ G$ has an independent set of size $\geq k$ .

For the forward direction, we suppoos that ${S_{i_{1}}, S_{i_{2}}, \dots, S_{i_{k}}}$ is a set packing:

For all p \neq = q : S_{i_{p}} \cap S_{i_{q}} = \emptyset ⟹ No edge (v_{i_{p}}, v_{i_{q}}) \in E ⟹ v_{i_{1}}, v_{i_{2}}, ..., v_{i_{k}} is an independent set in G

For the backward directoin, we supposed that ${v_{j_{1}}, v_{j_{2}}, \dots, v_{j_{k}}}$ is an indepenent set of $G$ .

For all p \neq = q : (v_{j_{p}}, v_{j_{q}}) \in / E ⟹ S_{j_{p}} \cap S_{j_{q}} = \emptyset (by construction) ⟹ S_{j_{1}}, S_{j_{2}}, ..., S_{j_{k}} is a set packing

Now to analyze its complexity:

Create m vertices: O (m) Check all pairs for intersection: O (m^{2} \cdot ∣ U ∣) Total: O (m^{2} \cdot ∣ U ∣) = polynomial in input size

Given that this reduction is computable in polynomial time(and also preserves solutions), we know:

SET - P A C K I NG \leq_{p} I N D EPEN D ENT - SET

Combining with hte result from class of INDEPENDENT-SET $\leq_{p}$ SET-PACKING, we now know:

SET - P A C K I NG \equiv_{p} I N D EPEN D ENT - SET

And thus the problems are computationally equivalent $■$ .

Graph View

Algo hw 12

Self Reducibility

Reduction to Decision Version

Set Packing and Independent Set

Constructing the Reduction