Homework 11 Written

---

Maximum Bipartite Matching: Maxflow Solution

Given the bipartite graph(Figure 1) shown below that we used in class, solve the problem of finding a maximum matching by reducing the problem to a maximum flow finding problem. Specifically, show the resulting flow network and residual graph after finding the maximum flow (using the basic Ford-Fulkerson algorithm). The flow network should show on every edge the flow value assigned and the capacity (e.g., f/c) and the residual graph should show on every edge the residual capacity. Additionally, write the maximum flow value and the minimum cut (e.g., ($\{s,a,b,c\},\{d,e,t\}$) resulting from the algorithm. Note the flow values on the individual edges of the flow network may vary a bit depending on the augmenting paths found randomly during the execution of the algorithm, but the maximum flow value is certainly the same and the minimum cut found is observably the same, too.

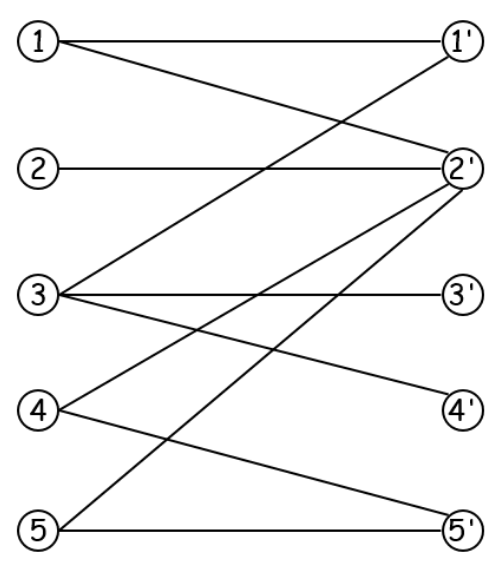
Initial Bipartite Graph Edges

$$\begin{array}{r}E=\{(1,1^{\prime }),(1,2^{\prime }),(2,2^{\prime }),(3,1^{\prime }),(3,2^{\prime }),\\ (3,3^{\prime }),(4,3^{\prime }),(4,4^{\prime }),(5,4^{\prime }),(5,5^{\prime })\}\end{array}$$

Construction of Flow Network

We add the source $s$ connected to all the leftside vertices $\{1,2,3,4,5\}$ with a capacity of 1. Then add a sink $t$ connected from all the rightside vertices $\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}$ with a capacity of 1. Thus all bipartite graph edges have a capacity of 1.

Execution of Ford-Fulkerson for Augmenting Paths

$$\begin{array}{rl}\text{Path 1:}& s\to 1\to 1^{\prime }\to t\text{(flow = 1)}\\ \text{Path 2:}& s\to 2\to 2^{\prime }\to t\text{(flow = 1)}\\ \text{Path 3:}& s\to 3\to 3^{\prime }\to t\text{(flow = 1)}\\ \text{Path 4:}& s\to 4\to 4^{\prime }\to t\text{(flow = 1)}\\ \text{Path 5:}& s\to 5\to 5^{\prime }\to t\text{(flow = 1)}\end{array}$$

Thus there exists no other augmenting pairs.

Final Resulting Network Flow

Source edges:

$$\begin{array}{rl}s\to 1& :1/1\\ s\to 2& :1/1\\ s\to 3& :1/1\\ s\to 4& :1/1\\ s\to 5& :1/1\end{array}$$

Bipartite Edges:

$$\begin{array}{rl}1\to 1^{\prime }& :1/1\text{ (in matching)}\\ 1\to 2^{\prime }& :0/1\\ 2\to 2^{\prime }& :1/1\text{ (in matching)}\\ 3\to 1^{\prime }& :0/1\\ 3\to 2^{\prime }& :0/1\\ 3\to 3^{\prime }& :1/1\text{ (in matching)}\\ 4\to 3^{\prime }& :0/1\\ 4\to 4^{\prime }& :1/1\text{ (in matching)}\\ 5\to 4^{\prime }& :0/1\\ 5\to 5^{\prime }& :1/1\text{ (in matching)}\end{array}$$

Sink edges:

$$\begin{array}{rl}{1}^{\prime }\to t& :1/1\\ 2^{\prime }\to t& :1/1\\ 3^{\prime }\to t& :1/1\\ 4^{\prime }\to t& :1/1\\ 5^{\prime }\to t& :1/1\end{array}$$

Residual Graph with only Residual Capacities

Forward Residual Edges:

$$\begin{array}{rl}s\to \{1,2,3,4,5\}& :0\text{ (all saturated)}\\ 1\to 2^{\prime }& :1\\ 3\to 1^{\prime }& :1\\ 3\to 2^{\prime }& :1\\ 4\to 3^{\prime }& :1\\ 5\to 4^{\prime }& :1\\ \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}\to t& :0\text{ (all saturated)}\end{array}$$

Backward Residual Edges:

$$\begin{array}{rl}\{1,2,3,4,5\}\to s& :1\text{ each}\\ 1^{\prime }\to 1& :1\\ 2^{\prime }\to 2& :1\\ 3^{\prime }\to 3& :1\\ 4^{\prime }\to 4& :1\\ 5^{\prime }\to 5& :1\\ t\to \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}& :1\text{ each}\end{array}$$

Results:

Max flow: 5

Max matching for $M$: $\{(1,1^{\prime }),(2,2^{\prime }),(3,3^{\prime }),(4,4^{\prime }),(5,5^{\prime })\}$ (with a perfect match)

Min Cut: $(\{s\},\{1,2,3,4,5,1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },t\})$

Thus, the cut with max capacity of 5 confirms the max flow flow/min cut theorem, where $MaxFlow=MinCutCapacity=5$

---

Software Porting

Do the textbook exercise 29 in Chapter 7. Show how to solve this problem by reformulating it to the problem of finding a minimum cut from a flow network built from the set $V$ of $n$ applications $v_1,v_2,\dots ,$ and $v_n$ in a manner similar to the approach used in the image segmentation problem (see Section 7.10). State clearly how a flow network is constructed for a given instance of the software porting problem.

Hint. One plausible way to construct a flow network from a software porting problem can be to let the source node s represent the new system and let the sink node $t$ represent the application 1 which cannot move to the new system. Then, there’s a parallel between the software porting problem and the image segmentation problem:

• The porting benefit $b_i$ of an application $i$ in the software porting problem parallels the foreground likelihood $a_i$ of a pixel $i$ in the image segmentation problem.
• The separation expense $x_{ij}$ between two applications $i$ and $j$ in the software porting problem (when only one of them is ported to the new system) parallels the separation penalty pij between two neighboring pixels $i$ and $j$ in the image segmentation problem (when one is in the foreground and the other is in the background).

Chapter 7 Exercise 29:

Some of your friends have recently graduated and started a small com- pany, which they are currently running out of their parents’ garages in Santa Clara. They’re in the process of porting all their software from an old system to a new, revved-up system; and they’re facing the following problem.

They have a collection of $n$ soft, rare applications, $\{1,2,\dots ,n\}$, running on their old system; and they’d like to port some of these to the new system. If they move application $i$ to the new system, they expect a net (monetary) benefit of $b_i\ge 0$. The different software applications interact with one another; if applications $i$ and $j$ have extensive interaction, then the company, will incur an expense if they move one of $i$ or $j$ to the new system but not both; let’s denote this expense by $x_{ij}\ge 0$.

So, if the situation were really this simple, your friends would just port all $n$ applications, achieving a total benefit of ${\sum }_i{b}_i$. Unfortunately, there’s a problem …

Due to small but fundamental incompatibilities between the two systems, there’s no way to port application 1 to the new system; it will have to remain on the old system. Nevertheless, it might still pay off to port some of the other applications, accruing the associated benefit and Incurring the expense of the interaction between applications on different systems.

So this is the question they pose to you: Which of the remaining applications, ff any, should be moved? Give a polynomial-time algorithm to find a set $S\subseteq \{2,3,\dots ,n\}$for which the sum of the benefits minus the expenses of moving the applications in $S$ to the new system is maximized.

Min Cut Solution

We know that $n$ applications $\{1,2,\dots ,n\}$, that application 1 cannot be ported as must stay on the old system, the benefits $b_i\ge 0$ for any porting application $i$, and seperation expenses $x_{ij}\ge 0$ if $i$ and $j$ are on different systems.

We first seek to find $S\subseteq \{2,3,\dots ,n\}$ to maximize:

$$\begin{array}{r}\text{Profit}(S)=\sum _{i\in S}{b}_i-\sum _{\begin{array}{c}i\in S,j\notin S\\ \text{or }j\in S,i\notin S\end{array}}{x}_{ij}\end{array}$$

We then define a new flow network construction where:

• $s$: source representing new system
• $t$ sink representing app 1 and old system
• $i\in \{2,3,\dots ,n\}$: note for each application

The edges and capacities can then be defined as:

$$\begin{array}{rl}\text{Type 1: }& s\to i\text{ for each }i\in \{2,3,\dots ,n\},\text{capacity }=b_i\\ \text{Type 2: }& i\to t\text{ for each }i\in \{2,3,\dots ,n\},\text{capacity }=x_{i1}\\ \text{Type 3: }& i\leftrightarrow j\text{ for each pair }i,j\in \{2,3,\dots ,n\},\text{capacity }=x_{ij}\end{array}$$

For the type 3 edges, we have to use undirected edges with a capacity of $x_{ij}$, which can be implemented as two directed edges: $i\to j$ witha capacity of $x_{ij}$ and $j\to i$ with capacity $x_{ij}$.

We can then define a cut $(A,B)$ as a separation of $s$ from $t$, where:

• $A$: $\{s\}\cup \{\text{applications ported to new system}\}$
• $B$: $\{t\}\cup \{\text{applications staying on old system with an app 1}\}$

We then let $S=A\cap \{2,3,\dots ,n\}$ be the product set of ported apps.

Calculating cut capacity with edges crossing $A$ to $B$:

$$\begin{array}{rl}\text{Cut capacity}& =\sum _{j\in B\setminus \{t\}}c(s,j)+\sum _{i\in S}c(i,t)+\sum _{\begin{array}{c}i\in S,j\in B\setminus \{t\}\end{array}}c(i,j)\\ & =\sum _{j\notin S,j\ge 2}{b}_j+\sum _{i\in S}{x}_{i1}+\sum _{\begin{array}{c}i\in S,j\notin S\\ i,j\ge 2\end{array}}{x}_{ij}\end{array}$$

We then connect the cut to objective by letting $B_{\text{total}}$ be the total benefit for all movable applications ${\sum }_{i=2}^n$, writing this as:

$$\begin{array}{rl}\text{Profit}(S)& =\sum _{i\in S}{b}_i-\left[\sum _{i\in S}{x}_{i1}+\sum _{\begin{array}{c}i\in S,j\notin S\\ i,j\ge 2\end{array}}{x}_{ij}\right]\\ & =\left(B_{\text{total}}-\sum _{j\notin S,j\ge 2}{b}_j\right)-\sum _{i\in S}{x}_{i1}-\sum _{\begin{array}{c}i\in S,j\notin S\\ i,j\ge 2\end{array}}{x}_{ij}\\ & =B_{\text{total}}-\left[\sum _{j\notin S,j\ge 2}{b}_j+\sum _{i\in S}{x}_{i1}+\sum _{\begin{array}{c}i\in S,j\notin S\\ i,j\ge 2\end{array}}{x}_{ij}\right]\\ & =B_{\text{total}}-\text{Cut capacity}(A,B)\end{array}$$

Yielding a final alogorithm of:

$$\begin{array}{rl}& \text{Algorithm: Software Porting via Min-Cut}\\ & \text{1. Construct flow network as described above}\\ & \text{2. Find minimum s-t cut using max-flow algorithm (e.g., Ford-Fulkerson)}\\ & \text{3. Let }S=\{i\in \{2,\dots ,n\}:i\text{ is on s-side of min-cut}\}\\ & \text{4. Return }S\text{ as the set of applications to port}\end{array}$$

With a time complexity of $O(m{n}^2)$ ( or $O(n^3)$ depending on maxflow algorithm), where m is num edges in the network.