Homework 5 Written

---

Prim’s MST Algorithm: Tracing

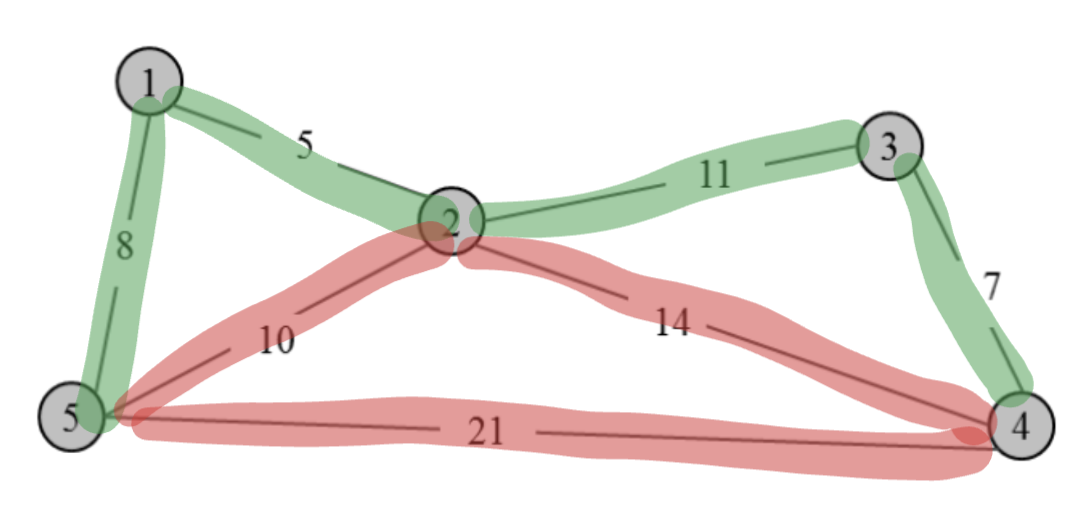
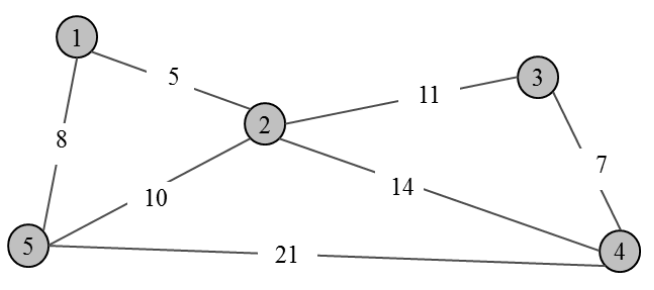
Run the Prim’s algorithm implemented using a priority queue (see below) against the graph shown below. Give your answers as follows.

1. Run the algorithm assuming the node a is picked as the start node s, and show the algorithm run trace (see the specification below).
2. Run the algorithm assuming the node g is picked as the start node s, and show the algorithm run trace (see the specification below).
3. Draw the resulting minimum spanning tree on the graph. Show the included edges in colored or thick lines.

Specification of the algorithm run tracing: For each algorithm run tracing, show the content of the cut $S$, the content of the $MSTT$, and the content of the priority queue $Q$ at the end of the While loop in each iteration. Specifically, show the content of $S$ as a set of nodes, the content of $T$ as a set of edges, and the content of $Q$ as a set of ordered pairs of a node number and a priority key. (For ease of grading, please show the end nodes of an edge in the alphabetical order (e.g., (a, d)), and list the priority queue elements in the alphabetic order of node number.) For example, when the start node is $a$, their contents before the 1st iteration is $S=\{\}$, $T=\{\}$, and $Q=\{(a,0),(b,\infty ),(c,\infty ),(d,\infty ),(e,\infty ),(f,\infty ),(g,\infty )\}$.

1. Starting at Node $a$

Let $i$ indicate iteration number.

$$\begin{array}{rl}Beforei& =1:\\ & S=\{\}\\ & T=\{\}\\ & Q=\{(a,0),(b,\infty ),(c,\infty ),(d,\infty ),(e,\infty ),(f,\infty ),(g,\infty )\}\\ Afteri& =1:\\ & S=\{a\}\\ & T=\{\}\\ & Q=\{(b,8),(c,5),(d,6),(e,\infty ),(f,\infty ),(g,\infty )\}\\ Afteri& =2:\\ & S=\{a,c\}\\ & T=\{(a,c)\}\\ & Q=\{(b,8),(d,6),(e,2),(f,4),(g,\infty )\}\\ Afteri& =3:\\ & S=\{a,c,e\}\\ & T=\{(a,c),(c,e)\}\\ & Q=\{(b,3),(d,6),(f,4),(g,\infty )\}\\ Afteri& =4:\\ & S=\{a,b,c,e\}\\ & T=\{(a,c),(b,e),(c,e)\}\\ & Q=\{(d,6),(f,4),(g,\infty )\}\\ Afteri& =5:\\ & S=\{a,b,c,e,f\}\\ & T=\{(a,c),(b,e),(c,e),(c,f)\}\\ & Q=\{(d,6),(g,1)\}\\ Afteri& =6:\\ & S=\{a,b,c,e,f,g\}\\ & T=\{(a,c),(b,e),(c,e),(c,f),(f,g)\}\\ & Q=\{(d,6)\}\\ Afteri& =7:\\ & S=\{a,b,c,d,e,f,g\}\\ & T=\{(a,c),(a,d),(b,e),(c,e),(c,f),(f,g)\}\\ & Q=\{\}\end{array}$$

2. Starting at Node $g$

Let $i$ indicate iteration number.

$$\begin{array}{rl}Beforei& =1:\\ & S=\{\}\\ & T=\{\}\\ & Q=\{(a,\infty ),(b,\infty ),(c,\infty ),(d,\infty ),(e,\infty ),(f,\infty ),(g,0)\}\\ Afteri& =1:\\ & S=\{g\}\\ & T=\{\}\\ & Q=\{(a,\infty ),(b,\infty ),(c,\infty ),(d,\infty ),(e,\infty ),(f,1)\}\\ Afteri& =2:\\ & S=\{f,g\}\\ & T=\{(f,g)\}\\ & Q=\{(a,\infty ),(b,\infty ),(c,4),(d,\infty ),(e,7)\}\\ Afteri& =3:\\ & S=\{c,f,g\}\\ & T=\{(c,f),(f,g)\}\\ & Q=\{(a,5),(b,10),(d,9),(e,2)\}\\ Afteri& =4:\\ & S=\{c,e,f,g\}\\ & T=\{(c,e),(c,f),(f,g)\}\\ & Q=\{(a,5),(b,3),(d,9)\}\\ Afteri& =5:\\ & S=\{b,c,e,f,g\}\\ & T=\{(b,e),(c,e),(c,f),(f,g)\}\\ & Q=\{(a,5),(d,9)\}\\ Afteri& =6:\\ & S=\{a,b,c,e,f,g\}\\ & T=\{(a,c),(b,e),(c,e),(c,f),(f,g)\}\\ & Q=\{(d,6)\}\\ Afteri& =7:\\ & S=\{a,b,c,d,e,f,g\}\\ & T=\{(a,c),(a,d),(b,e),(c,e),(c,f),(f,g)\}\\ & Q=\{\}\end{array}$$

3. MST Drawing

---

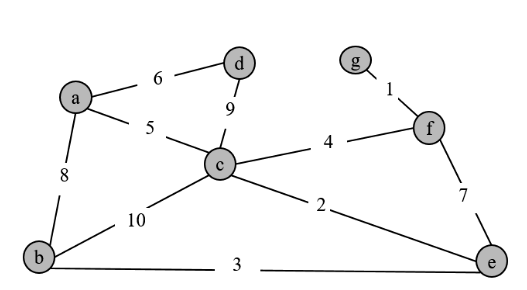
Kruskal’s MST Algorithm Tracing

Run the Kruskal’s MST algorithm shown below (left) on the graph shown below (right), using disjoint sets data structure represented as a forest. Provide your answer as instructed below.

1. List the edges after the sorting (format: “(v1, v2), (v3, v4),…”).
2. Draw the forest structure after MakeUnionFind.
3. In each iteration of the ‘for’ loop, write the trace of Find and Union operations (e.g., “Find(v) returns u.”, “Do Union(v1, v2).”, “Discard (v1, v2).”), and draw the resulting forest structure. Use the union-by-size heuristic for Union.
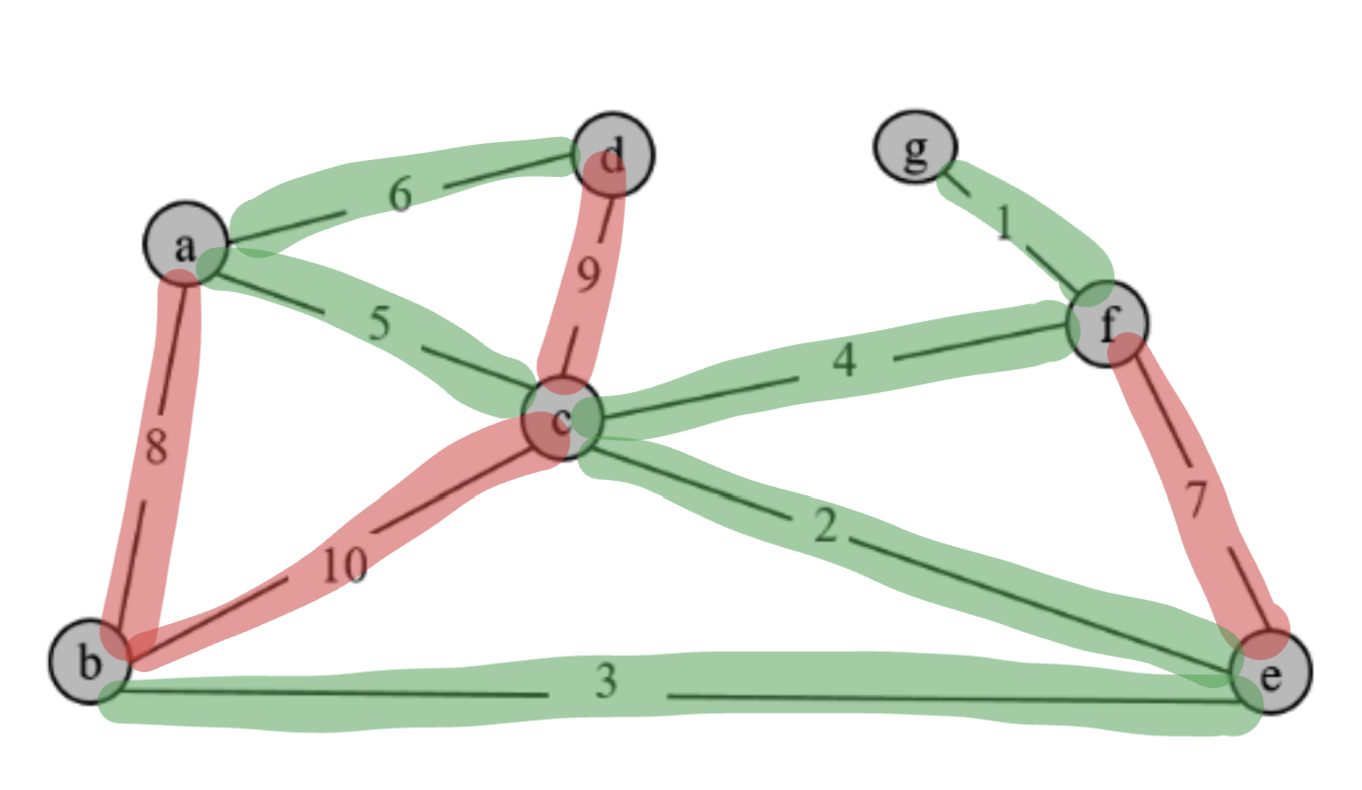
4. After the algorithm terminates, draw the final MST of the graph (by making the included edges thicker or red). (There is no need to show the MST in every iteration.)

Please follow this specification for the consistency and convenience of grading:

• Iterate the ‘for’ loop over all edges (without an early termination), as written in the algorithm.
• When drawing a forest, show the trees in an increasing order of the root node number.
• If the disjoint sets do not change in an iteration, you do not need to show the forest structure.
• If two trees that are merged have the same size, make the second tree (on the right) a subtree of the first tree (on the left).

1. Sorting the Edgeso

Sorting the edges yields:

$$(1,2),(3,4),(1,5),(2,5),(2,3),(2,4),(4,5)$$

2. Resulting Forest Structure from $MakeUnionFind$

This just yields each node having its own tree with a size of $1$:

$$12345$$

3. Iterating over Traces

Once again letting $i$ indicate iteration.

$$\begin{array}{rl}Iterationi& =1:\text{ Edge }(1,2)\text{ with weight }5\\ & \text{Find}(1)\text{ returns }1.\\ & \text{Find}(2)\text{ returns }2.\\ & \text{Do Union}(1,2).\\ & T=\{(1,2)\}\\ & \\ Iterationi& =2:\text{ Edge }(3,4)\text{ with weight }7\\ & \text{Find}(3)\text{ returns }3.\\ & \text{Find}(4)\text{ returns }4.\\ & \text{Do Union}(3,4).\\ & T=\{(1,2),(3,4)\}\\ & \\ Iterationi& =3:\text{ Edge }(1,5)\text{ with weight }8\\ & \text{Find}(1)\text{ returns }1.\\ & \text{Find}(5)\text{ returns }5.\\ & \text{Do Union}(1,5).\\ & T=\{(1,2),(3,4),(1,5)\}\\ & \\ Iterationi& =4:\text{ Edge }(2,5)\text{ with weight }10\\ & \text{Find}(2)\text{ returns }1.\\ & \text{Find}(5)\text{ returns }1.\\ & \text{Discard }(2,5).\\ & T=\{(1,2),(3,4),(1,5)\}\\ & \\ Iterationi& =5:\text{ Edge }(2,3)\text{ with weight }11\\ & \text{Find}(2)\text{ returns }1.\\ & \text{Find}(3)\text{ returns }3.\\ & \text{Do Union}(1,3).\\ & T=\{(1,2),(3,4),(1,5),(2,3)\}\\ & \\ Iterationi& =6:\text{ Edge }(2,4)\text{ with weight }14\\ & \text{Find}(2)\text{ returns }1.\\ & \text{Find}(4)\text{ returns }1.\\ & \text{Discard }(2,4).\\ & T=\{(1,2),(3,4),(1,5),(2,3)\}\\ & \\ Iterationi& =7:\text{ Edge }(4,5)\text{ with weight }21\\ & \text{Find}(4)\text{ returns }1.\\ & \text{Find}(5)\text{ returns }1.\\ & \text{Discard }(4,5).\\ & T=\{(1,2),(3,4),(1,5),(2,3)\}\end{array}$$

4. Final MST