Homework 4 Written

Minimum Max-lateness Job Scheduling

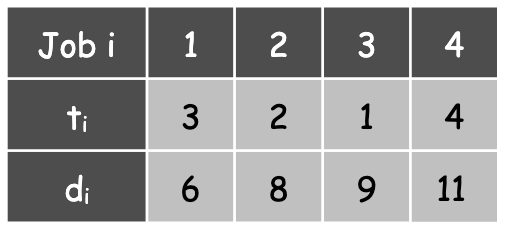
Consider the four jobs ( $J o bi, i = 1, 2, 3, 4$ ) in the table below, where $t_{i}$ is the processing time and $d_{i}$ is the deadline of each Job $i$ . Show a job schedule that is optimal but does not follow the earliest-deadline-first strategy and contains at least one adjacent inversion. Then, repeatedly remove inversions until we have an optimal schedule that can be generated using the earliest-deadline-first strategy. Show the job schedule after removing each inversion.

Getting the obvious out of the way, we know the earliest-deadline-first strategy would yield:

J o b 1 \to J o b 2 \to J o b 3 \to J o b 4

Let’s start with an optimal scheule by use of inversions and then remove them one at a time:

starting schedule J o b 2 \to J o b 3 \to J o b 1 \to J o b 4

To verify that this an an optimal scheduling we can verify the jobs are completed before their deadline(assume list number represents job #):

completes with a time of $3 + 3 = 6$ , where deadline is $6$
completes at time $2$ , where deadline is $8$
completes at time $2 + 1 = 3$ , where deadline is $9$
completes at time $6 + 4 = 10$ , where deadline is $11$

No lateness, so it is optimal.

We now check for adjacent inversions $J o b_{2} \to J o b_{3}, J o b_{3} \to J o b_{1}, J o b_{1} \to J o b_{4}$ :

$J o b_{2}$ with $J o b_{3}$ has no inversion since $8 < 9$ . $J o b_{3}$ with $J o b_{1}$ does have inversion as $9 > 6$ . $J o b_{1}$ with $J o b_{4}$ does not have inversion as $6 < 11$

We remove inversion by swapping $J o b_{3}$ and $J o b_{1}$ , yielding:

J o b_{2} \to J o b_{1} \to J o b_{3} \to J o b_{3}

Verifying again:

completes with a time of $2 + 3 = 5$ , where deadline is $6$
completes at time $2$ , where deadline is $8$
completes at time $5 + 1 = 6$ , where deadline is $9$
completes at time $6 + 4 = 10$ , where deadline is $11$

Next inversions for $J o b_{2} \to J o b_{1}, J o b_{1} \to J o b_{3}, J o b_{3} \to J o b_{4}$ :

$J o b_{2}$ with $J o b_{1}$ does have inversion as $8 > 6$ . $J o b_{1}$ with $J o b_{3}$ does not have inversion as $6 < 9$ . $J o b_{3}$ with $J o b_{4}$ does not have inversion as $9 > 11$ .

We remove inversion by swapping $J o b_{2}$ and $J o b_{1}$ , yielding:

J o b_{1} \to J o b_{2} \to J o b_{3} \to J o b_{4}

We could verify, but we have now reached the earliest deadline first schedule and the deadlines are ordered.

Dijkstra’ Algorithm Tracing

Show the tracing of executing Dijkstra’s single-source shortest paths algorithm given below on the undirected graph given below. (We discussed this algorithm implementation in class.)

apologies if I did the drawing process incorrectly, I didnt understand the directions perfectly. I made one mistake merging two iterations together, but difficult to recover/fix unforunately.