Homework 2 - DFA and NFA Construction

---

BFS Tree and DFS Tree Properties

(Modified from a textbook exercise.) Consider a connected graph $G=(V,E)$ and consider a vertex $u\in V$. Suppose we are doing breadth-first search and depth-first search traversals on the graph $G$ starting with the node $u$, and further suppose that the breadth-first search tree and the depth-first search resulting from the two traversals are the same tree $T$. Prove that in that case $G=T$, that is, $G$ does not contain any edge that does not belong to T. Hint: Property 3.4 (for BFS tree) and Property 3.7 (for DFS tree). Suggested proof technique: by contradiction.

Given our connected graph $G=(V,E)$ where $u\in V$, first run $BFS$ and $DFS$ algorithms start from $u$.

We will also define a spanning tree $T$ such that both the $BFS$ and $DFS$ are $T$. We seek to show that $G=T$, meaning there is no edge from $G$ not in $T$.

As a setup for contradiction, let us assume that there is some edge $e=(x,y)\in E$ that also is not in $E(T)$

We will also let $x$ be in $BFS$ layer $L_i$ and let $y$ be in $BFS$ layer $L_j$.

Considering the edge $e$ that is not in $T$. Given that $T$ is the BFS tree, by the $BFS$ Property (3.4), we know that:

$$|i-j|\le 1$$

Leaving us with two possibilities $i=j$(1) or $|i-j|=1$(2)

1. If this is the case, that means that both $x$ and $y$ are on the same level in the $BFS$ tree. However, this is impossible given that ancestors and descendants must have different depths, forcing a contradiction.
2. If this is the case, we can let $j=i+1$. Naturally this means that one of these is an ancestor of the other. But their depths are $1$ apart, so one must be the direct child of the other. Given this parent/child edge that is part of $T$, that means that $(x,y)$ IS a tree edge, and thus the statement $(x,y)\notin E(t)$ is contradicted.

Since both possibilities lead to contradiction, therefore every edge $G$ must be in $T$, $G=T$ $■$

---

All Topological Orders

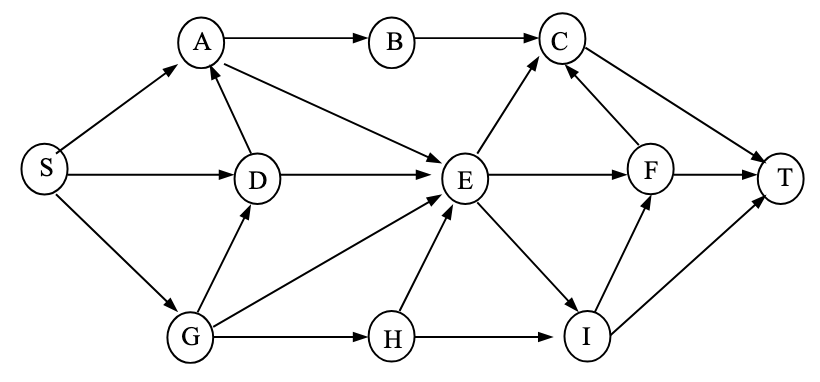
Given the DAG below, list all possible topological orders and state how many there are. Do it manually (it won’t take too long). Additionally, run any Java program code you can obtain to verify the manually run result (you can use any data structure to represent the graph); cite the source of the program code (e.g., URL) in the homework answer, and submit the code as a separate file. (This is not a programming exercise but part of a written exercise.)

I was able to find 13 possible combinations. Unfortunately I did not handwrite this assignment, so there is no proof of work. I will provide a trace diagram to show SOME element of work.

1. S G D A B H E I F C T
2. S G D A H B E I F C T
3. S G D A H E B I F C T
4. S G D A H E I B F C T
5. S G D A H E I F B C T
6. S G D H A B E I F C T
7. S G D H A E B I F C T
8. S G D H A E I B F C T
9. S G D H A E I F B C T
10. S G H D A B E I F C T
11. S G H D A E B I F C T
12. S G H D A E I B F C T
13. S G H D A E I F B C T

My rough procedure:

1. remove node $S$
2. remove node $G$
3. remove node $D$
4. remove node $A$
5. remove node $H$
6. remove node $B$
7. remove node $B$
8. remove node $I$
9. remove node $F$

Decision Tree Diagram: see figure 2

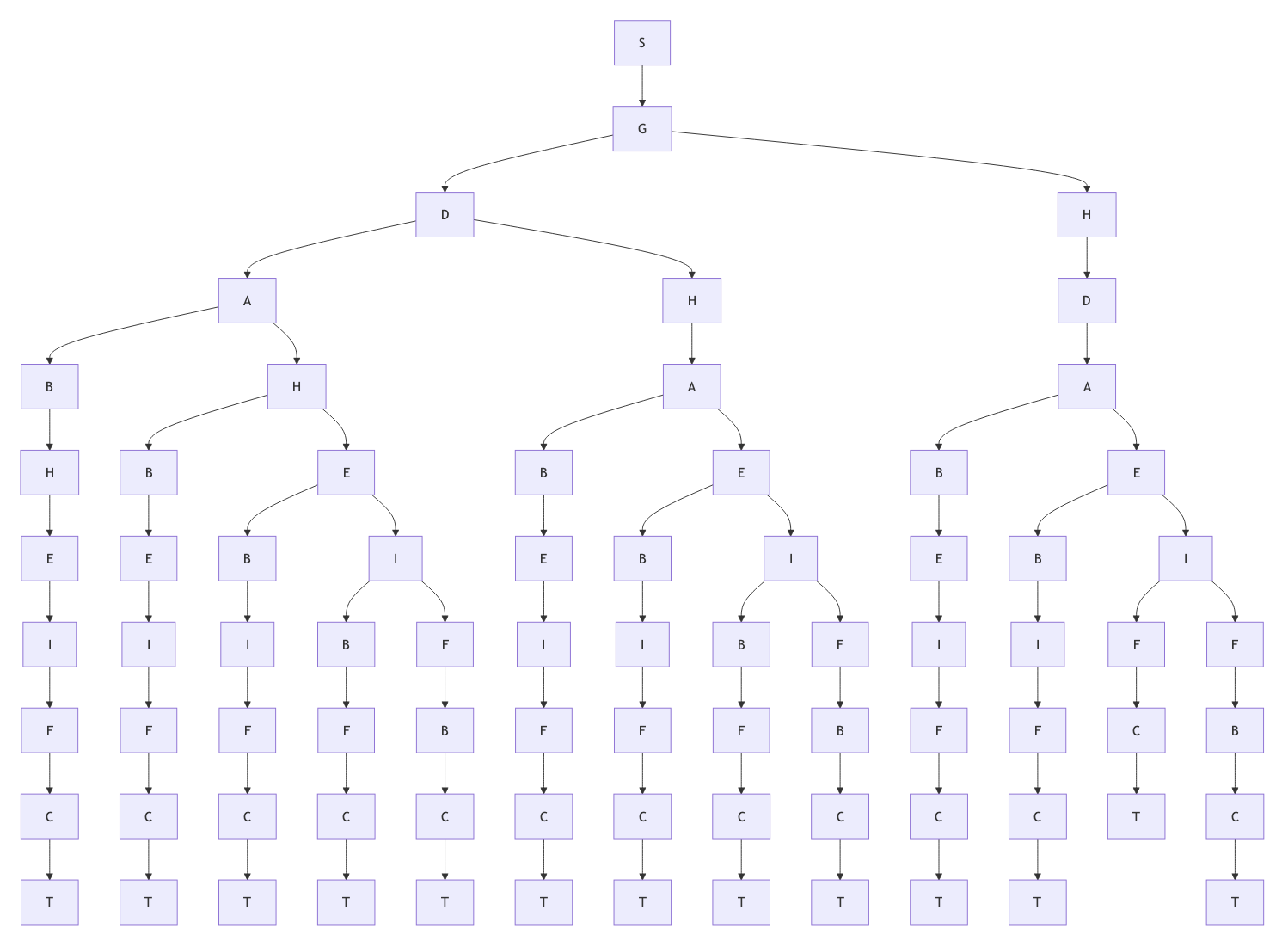
For the code, I used GeeksForGeeks’¹ implementation. This implementation worked on numbers nodes, so I just used the mapping $0-10$:

$$0=S,1=G,2=D,3=A,4=B,5=H,6=E,7=I,8=F,9=C,10=T$$

GeeksForGeeks’ code with our graph set:

import java.util.*;
 
class Graph {
    int V;
    List<Integer> adjListArray[];
    private int count = 0;
 
    public Graph(int V) {
        this.V = V;
        @SuppressWarnings("unchecked")
        List<Integer> adjListArray[] = new LinkedList[V];
        this.adjListArray = adjListArray;
        for (int i = 0; i < V; i++) {
            adjListArray[i] = new LinkedList<>();
        }
    }
 
    public void addEdge(int src, int dest) {
        this.adjListArray[src].add(dest);
    }
    
    private void allTopologicalSortsUtil(boolean[] visited, 
                        int[] indegree, ArrayList<Integer> stack) {
        boolean flag = false;
 
        for (int i = 0; i < this.V; i++) {
            if (!visited[i] && indegree[i] == 0) {
                visited[i] = true;
                stack.add(i);
                for (int adjacent : this.adjListArray[i]) {
                    indegree[adjacent]--;
                }
                allTopologicalSortsUtil(visited, indegree, stack);
                visited[i] = false;
                stack.remove(stack.size() - 1);
                for (int adjacent : this.adjListArray[i]) {
                    indegree[adjacent]++;
                }
                flag = true;
            }
        }
        if (!flag) {
            for (int idx = 0; idx < stack.size(); idx++) {
                System.out.print(stack.get(idx));
                if (idx < stack.size() - 1) System.out.print(" ");
            }
            System.out.println();
            count++;
        }
    }
    
    public void allTopologicalSorts() {
        boolean[] visited = new boolean[this.V];
        int[] indegree = new int[this.V];
 
        for (int i = 0; i < this.V; i++) {
            for (int var : this.adjListArray[i]) {
                indegree[var]++;
            }
        }
 
        ArrayList<Integer> stack = new ArrayList<>();
        allTopologicalSortsUtil(visited, indegree, stack);
        System.out.println("\nTotal topological orders: " + count);
    }
 
    public static void main(String[] args) {
        Graph graph = new Graph(11);
 
        graph.addEdge(0, 3); // S -> A
        graph.addEdge(0, 2); // S -> D
        graph.addEdge(0, 1); // S -> G
 
        graph.addEdge(1, 2); // G -> D
        graph.addEdge(1, 6); // G -> E
        graph.addEdge(1, 5); // G -> H
 
        graph.addEdge(2, 3); // D -> A
        graph.addEdge(2, 6); // D -> E
 
        graph.addEdge(3, 4); // A -> B
        graph.addEdge(3, 6); // A -> E
 
        graph.addEdge(4, 9); // B -> C
 
        graph.addEdge(6, 9); // E -> C
        graph.addEdge(6, 8); // E -> F
        graph.addEdge(6, 7); // E -> I
 
        graph.addEdge(5, 7); // H -> I
        graph.addEdge(5, 6); // H -> E
 
        graph.addEdge(7, 8); // I -> F
        graph.addEdge(7, 10); // I -> T
        graph.addEdge(8, 9); // F -> C
        graph.addEdge(8, 10); // F -> T
 
        graph.addEdge(9, 10); // C -> T
 
        graph.allTopologicalSorts();
    }
}

Footnotes

1. https://www.geeksforgeeks.org/dsa/all-topological-sorts-of-a-directed-acyclic-graph/?utm_source=chatgpt.com ↩