Homework 1 Written

---

Adjacency Matrix and Adjacency List

Consider the directed graph shown below.

1. Show both an adjacency matrix representation and an adjacency list representation of the graph. A node is not adjacent to itself unless there is a self-loop.
2. For each of the adjacency matrix and adjacency list representation of the graph in the exercise a, write in pseudocode the algorithm of a function Find_all_edges that outputs all edges in the graph, and show its big-O run-time complexity – make sure to show the steps of deriving the run-time complexity; no point will be given to an answer without the steps.

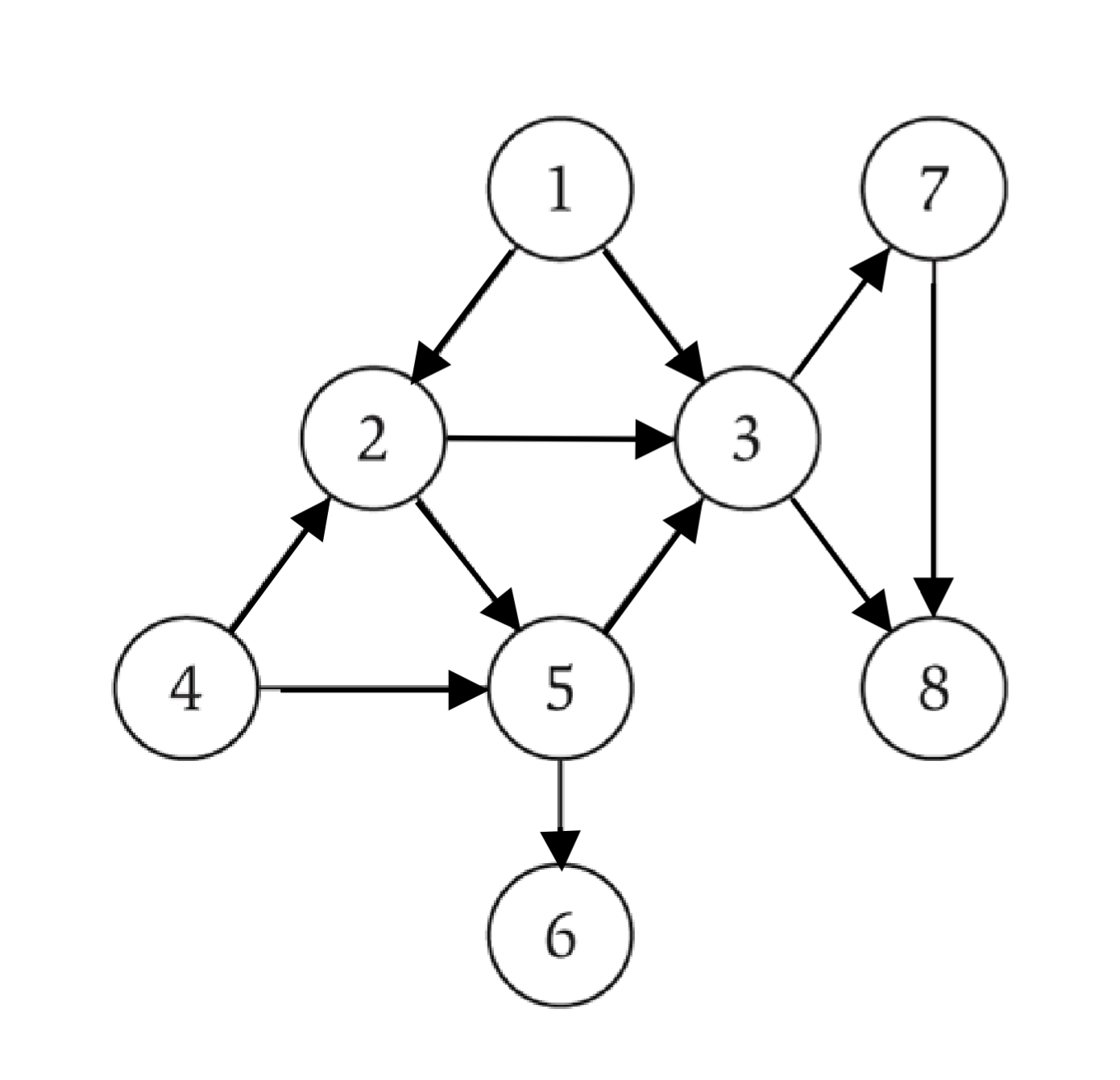
1. Adjacency Matrix and Adjacency List

The adjacency matrix representation of the graph is as follows:

this is assuming node number corresponds to index c-1 in the matrix

$$A=\left[\begin{array}{cccccccc}0& 1& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 1& 0& 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right]$$

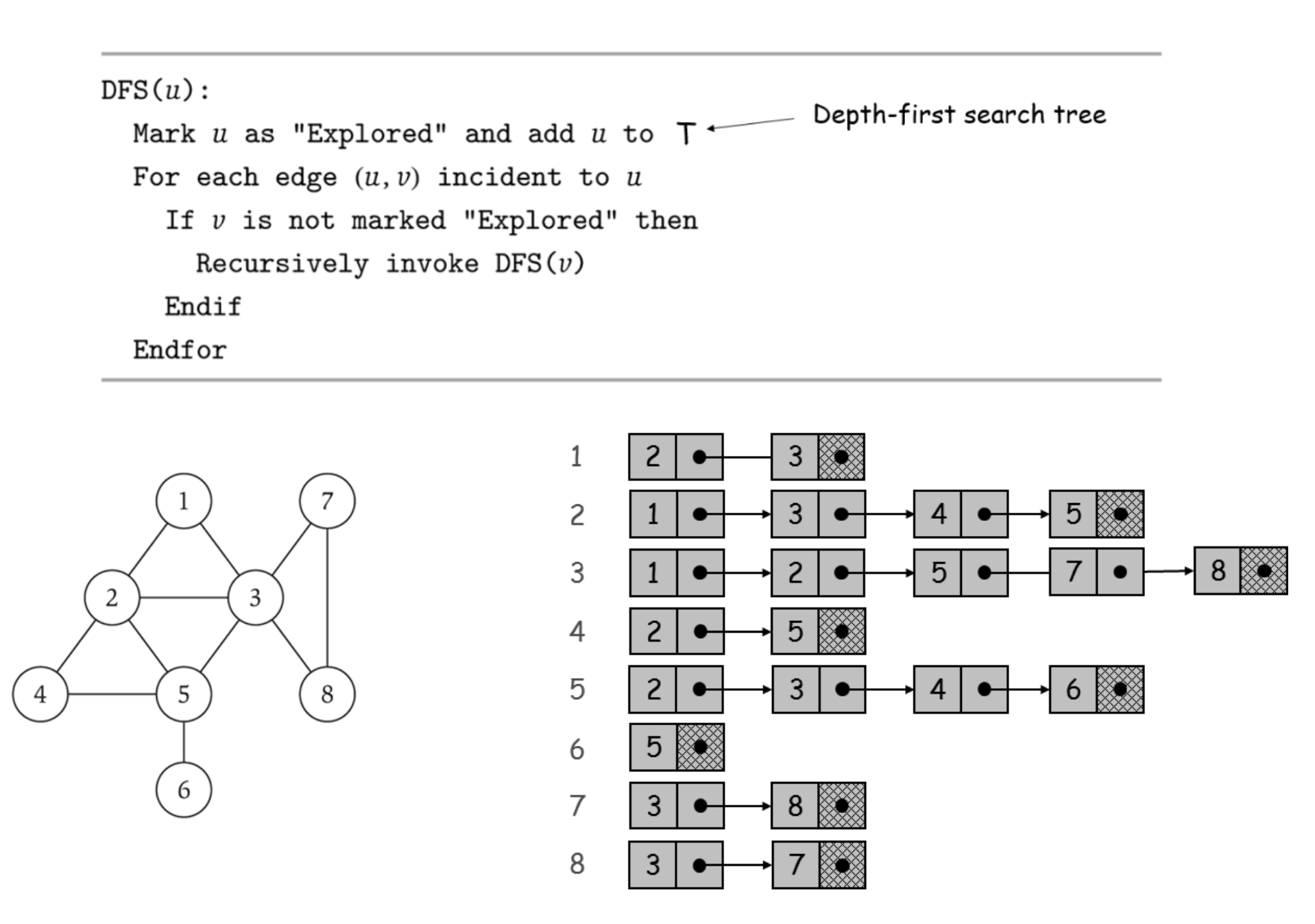
For the adjacency list, see figure 2, where red index represents an unreachable point.

2. Pseudocode Algorithms

This one is $O(n^2)$, as there are two nested $for$ loops iterating over the whole set of vertices.

This one is $O(n+k)$, as while there are two $for$ loops, the second one one iterates over all $v$ that are in the subset of $G[i]$

---

Depth-first Search: Algorithm Tracing

Consider the recursive depth-first search algorithm, the graph, and its adjacency list representation shown below. Consider the nodes in a linked list of the adjacency list in the order from left to right exactly as shown. (Note that, at each recursive call, there can be only one possible node to be invoked upon, that is, the first node in the linked list.) Do algorithm tracing on the graph twice: once for the start node 2 and once for the start node 6, and show the tracing outputs for each. The tracing output should include the sequence of recursive calls and returns from those calls in the following format: “call DFS(a); call DFS(b); call DFS(c); return from DFS(c); call DFS(d); return from DFS(d); return from DFS(b); return from DFS(a)”. Additionally, show the depth-first search tree resulting from each run of the algorithm for the different start nodes; use the format shown in Figure 3.5(g) of the textbook (page 85). Note this is not a programming exercise but a written exercise.

Node 2

Traced Output

call DFS(2); call DFS(1); call DFS(3); call DFS(5); call DFS(4);
return from DFS(4); call DFS(6); return from DFS(6); return from DFS(5);
call DFS(7); call DFS(8); return from DFS(8); return from DFS(7);
return from DFS(3); return from DFS(1); return from DFS(2)

DFS Tree Diagram

created with mermaid

Node 6

Traced Output

call DFS(6); call DFS(5); call DFS(2); call DFS(1); call DFS(3); call DFS(7); call DFS(8); return from DFS(8); return from DFS(7);
return from DFS(3); return from DFS(1); call DFS(4);
return from DFS(4); return from DFS(2); return from DFS(5); return from DFS(6)

DFS Tree Diagram

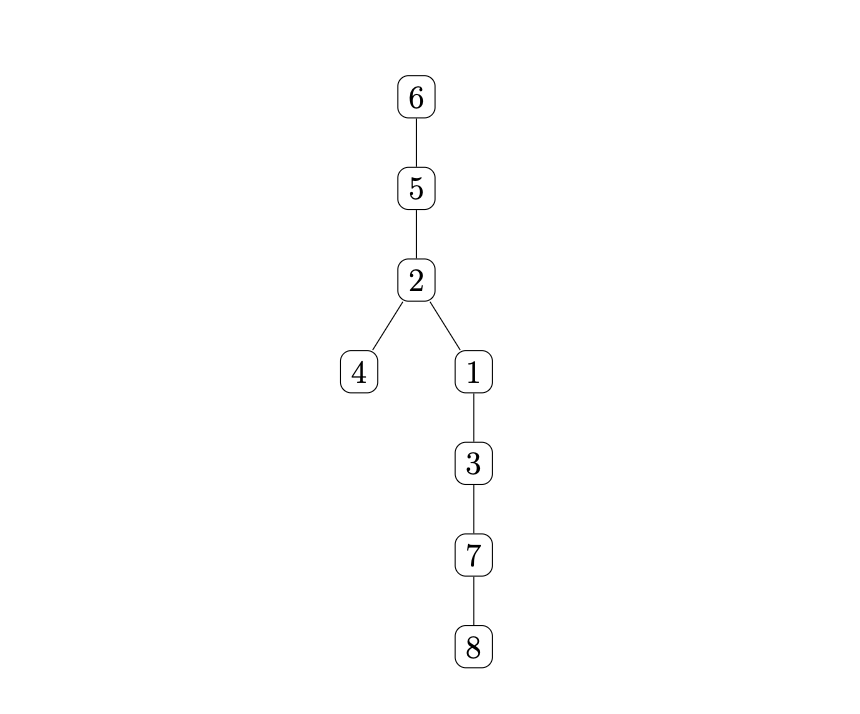
created with mermaid